image
Home Journals Progress in Chemistry
Progress in Chemistry

Abbreviation (ISO4): Prog Chem      Editor in chief: Jincai ZHAO

About  /  Aim & scope  /  Editorial board  /  Indexed  /  Contact  / 
Online first  /  Current issue  /  All issues  /  Top access  /  RSS

Progress in Chemistry >

2024 , Vol. 36 >Issue 9: 1412 - 1424

DOI: https://doi.org/10.7536/PC240313

Review

Principle and Application of Algae Concentration Prediction Models in Lakes and Reservoirs

  • Yuxuan Xie 1 ,
  • Jun Wang 1 ,
  • Yuqing Tang 2 ,
  • Yun Zhu 3 ,
  • Zehui Tian 2 ,
  • Alex T. Chow 4 ,
  • Chao Chen , 1, 5, *
Expand
  • 1 School of Environment, Tsinghua University, Beijing 100084, China
  • 2 Tangshan Water Supply Co., Tangshan 063000, China
  • 3 School of Environmental Science and Engineering, Suzhou University of Science and Technology, Suzhou 215009
  • 4 Earth and Environmental Sciences Programme, The Chinese University of Hong Kong, Hong Kong 999077, China
  • 5 Research Institute for Environmental Innovation (Suzhou) Tsinghua, Suzhou 215163, China
*e-mail:

Received date: 2024-03-08

  Revised date: 2024-04-03

  Online published: 2024-07-01

Supported by

Key Technology Research and Development Program of Shandong(2020CXGC011406)

National Natural Science Foundation of China(22076091)

“One river, one plan, one map, one list analysis and emergency drill service of key rivers in Chengdu”(N5101012023000142-1)

Fold

Abstract

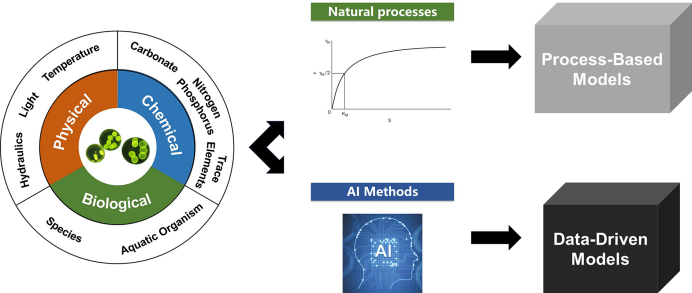
the risk of algal blooms has significantly increased in eutrophic lakes and reservoirs due To the global climate change and anthropogenic pollution,which has a significant impact on the safety and stability of municipal water supplies.to protect source water,it is necessary to construct a mathematical model and alert system to predict algae concentration in lakes and reservoirs.This paper reviews the main environmental factors(physical,chemical,and biological)that affect the algae growth,and summarizes the principles and application scenarios of existing models.Prediction models can generally be divided into two categories:process-based models(PB models)and data-driven models(DD models).PB models are based on natural processes,which enhances their interpretability and generality.However,they require a high level of research and testing,which can be costly.DD models rely on artificial intelligence methods such as machine learning,which offer flexible and diverse modeling approaches.However,they depend on data quality,lack mechanism support,and are location-specific.Both models have been extensively studied in the past decades and have been applied in some lakes and reservoirs.to further improve model performance,future research should improve the frequency and quality of data monitoring and combine natural process mechanisms with artificial intelligence methods。

Contents

1 Introduction

1.1 Eutrophication

1.2 Impacts of algal blooms

2 Influencing Factors

2.1 Physical factors

2.2 Chemical factors

2.3 Biological factors

3 Algae concentration prediction model

3.1 Process-based models

3.2 Data-driven models

3.3 Pro and cons

4 Conclusion and suggestions

Key words： lakes and reservoirs; algal blooms; influencing factors; algae concentration prediction; process-based models; data-driven models

Cite this article

Yuxuan Xie , Jun Wang , Yuqing Tang , Yun Zhu , Zehui Tian , Alex T. Chow , Chao Chen . Principle and Application of Algae Concentration Prediction Models in Lakes and Reservoirs[J]. Progress in Chemistry, 2024 , 36(9) : 1412 -1424 . DOI: 10.7536/PC240313

1 Introduction

1.1 Eutrophication and water bloom

Lakes and reservoirs are an important part of drinking water sources at home and abroad.According to statistics,in recent years,the number of centralized drinking water sources in lake-reservoir cities in China has increased to 40.6%,and the proportion of serving population has reached 47.2%[1]。 There is a widespread situation of continuous excessive input of external nutrient sources in lake and reservoir water sources,and most of them are facing different degrees of eutrophication[2]。 From 1986 to 2020,the eutrophication of 146 lakes over 10 km2in eastern China increased with the increase of human activities[3]。 Remote sensing satellite data show that in the past 30 years from 1984 to 2012,more than 2/3 of the 71 lakes(48 lakes)in 6 continents except Antarctica have increased the intensity of summer blooms[4]。
water bloom is a phenomenon that algae grow and reproduce in large quantities in a short time,forming visible aggregates on the water surface,resulting in water discoloration,of which cyanobacteria bloom is the most typical[5,6]。 algal blooms are closely related to the aggravation of water eutrophication and global warming.in recent years,human activities have significantly increased the global temperature and the input rate of nutrients In water sources.When the water temperature rises and the concentration of nitrogen and phosphorus exceeds a certain threshold,it is easy to cause ecological imbalance and Algal blooms[7][8,9][10][11,12]。

1.2 Effects of Algal Blooms

Algal blooms have a serious impact on water quality and aquatic ecology,which not only reduce water transparency and inhibit the photosynthesis of submerged plants,but also promote the reproduction of bacteria and other microorganisms,consume a large amount of dissolved oxygen in water,lead to the death of aquatic animals and plants,change the species composition of aquatic systems,and cause water quality deterioration[13]。 water blooms may also destroy the ornamental value of landscape Water bodies and have an impact on tourism and aquaculture[14]。
water bloom will also have adverse effects on all aspects of the water supply system.algae organic matter will consume coagulant,affect the effect of coagulation and sedimentation,Algae cells will block or penetrate the filter,increase the intensity and frequency of backwashing,affect the biological stability of the water supply network,and is not conducive to the normal operation of the waterworks[15]。 Algae organic matter is not only an important precursor of conventional disinfection by-products such as trihalomethanes and haloacetic acids,but also a precursor of new disinfection by-products such as nitrosamines,haloacetonitriles and haloamides[16,17]。 In addition,algal cells contain a large number of proteinaceous nitrogenous organic compounds.Studies have shown that nitrogenous organic compounds such as amino acids and peptone can form dimethylnitrosamine(NDMA)precursors under the action of microorganisms.For example,alanine can be methylated during microbial metabolism to form dialkylamine structures[18][19][20]。 Therefore,the outbreak of algal blooms will seriously affect the disinfection process,which will not only consume a large number of disinfectants and increase the cost of agent dosing,but also may produce a large number of conventional or new disinfection by-products,increasing the safety risk of residential water use。
toxic and odorous substances produced by algal blooms are common problems facing drinking water safety in recent years.Some cyanobacteria can secrete Toxic substances such as algal toxins,which seriously endanger the safety of water supply.for example,in the summer of 2014,the water supply in Toledo,Ohio,was interrupted For 3 days due to Microcystis blooms,affecting the normal water use of more than 400,000 residents[21]。 Davis et al.Also showed that the increase of temperature and phosphorus concentration contributed to the growth of toxic strains of Microcystis,which means that the trend of eutrophication and climate warming may lead to the outbreak of more toxic Microcystis blooms[22]。 Among the odor substances,2-methylisoborneol(2-MIB)and geosmin not only have very low odor threshold,but also are not easy to be removed by conventional processes,and cyanobacteria are considered to be the main source of these two odor substances[23,24][25]。 For example,the Miyun Reservoir in Beijing has a long-standing odor problem caused by MIB[26]。 in June 2007,a serious Anabaena spiroides bloom broke out In the water source area of Qinhuangdao,releasing high concentrations of geosmin[27]。 When the dead algae are degraded under anaerobic conditions,they will produce mercaptans,thioethers and other malodorous substances.in May 2007,a large number of dead cyanobacteria on the north shore of Taihu Lake produced high concentrations of mercaptan thioethers,which led to a strong odor in the tap water of Wuxi residents and triggered a drinking water crisis in the city[28,29]。 water blooms in different seasons also have different odor characteristics,and the odor problems of drinking water caused by the large growth of dinoflagellates,diatoms,cryptophytes and other algae adapted to the low water temperature environment in winter and spring have also been reported.Unlike cyanobacteria,aldehydes are the main odor substances[30,31]。
In the context of global climate change,blooms may become the greatest inland water quality threat to public health and aquatic ecosystems[32]。 the risk of algal blooms in eutrophic water sources persists,and algal toxins and odor substances are one of the important reasons for the deterioration of water quality in water supply sources such as lakes and reservoirs,and their impacts are usually sudden,diverse,and hidden,which is a major challenge in the current water supply field[33]。
Based on the global eutrophication of lakes and reservoirs and the serious impact of algal blooms,it is particularly important to identify the key factors inducing algae growth,construct a quantitative mathematical model of algae concentration,establish an early warning and emergency response system for algal blooms,and formulate targeted prevention and control measures。

2 Main factors affecting the growth of algae

the growth of algae in water source area is affected by many factors,and the growth of algae will react on some of the influencing factors,forming a complex interactive network.the prediction model is essentially to construct the mathematical correspondence between algae concentration and impact factor.Generally speaking,the impact factors can be divided into three categories:physical,chemical and biological factors,as shown in Figure 1[34]。
图1 影响藻类生长的主要因素

Fig. 1 Main factors affecting algae growth

2.1 Physical factor

Physical factors mainly include climate and hydraulic factors,such as temperature,light,hydrodynamic conditions,etc。
temperature affects biochemical reaction rates and is usually quantified by the Arrhenius equation.Within a certain range,the increase of temperature is conducive to the growth and metabolism of thermophilic cyanobacteria and green algae,and the water temperature around 27℃is considered to be the optimal growth temperature for cyanobacteria and green algae[35]。 the optimum growth temperature of dinoflagellates and diatoms is obviously lower,so they have more competitive advantages in The low temperature environment in winter and spring[36]。
light directly affects the photosynthetic rate of algae cells,which can be divided into three ranges according to the light intensity:light limitation,light saturation and photoinhibition.Laboratory experiments show that the optimal light intensity of various algae species is distributed in the range of 3 000~13 000 lx when other growth conditions are suitable[37][38]。 different algae species have Different adaptability to light,for example,cyanobacteria can use weak light more effectively than green algae and diatoms,and their unique phycobiliprotein also makes cyanobacteria have a wider light absorption band,thus showing a stronger competitive advantage under low light intensity[39][40]。 the light intensity available to algae cells in actual water is also affected by water turbidity and water depth,solar radiation will be attenuated when penetrating the water,and the attenuation rate of light radiation in different wavelength ranges is also different.Therefore,the higher the turbidity or the deeper the water level,the weaker the light intensity.Laboratory and field studies have shown that raising the water level or increasing the turbidity may help to reduce the odor problems caused by benthic cyanobacteria[41][42,43]。
hydrodynamic conditions are affected by water temperature,wind speed,rainfall,water depth and many other factors,which not only affect the growth of algae,but also affect the eutrophication level of water body.the effect of Hydrodynamic conditions on algae is not linear,and the growth of algae can be inhibited above or below a certain critical value[44]。 the critical value is related to the selection of hydraulic indexes,the type of algae species and the nutritional conditions of the water body.Taking the flow velocity index as an example,the results of laboratory and field tests and model simulation show that 0.04~0.5 m/s is the critical flow velocity for the growth of phytoplankton[45⇓~47]。 More studies tend to control algal blooms by increasing flow velocity and decreasing hydraulic retention time[48,49]。

2.2 Chemical factor

Chemical factors mainly include water quality and atmospheric components,such as total nitrogen,total phosphorus,carbonate system(pH value,alkalinity and CO2concentration)and trace elements 。
nitrogen and phosphorus are the main nutrient elements for algae growth,and also the main factors for evaluating the eutrophication level of water body.Monod equation or Droop equation is often used to describe the kinetic effects of Nitrogen and phosphorus on algae growth.According to Liebig's law of minimum factor,some studies only consider the limiting factors[50]。 the effects of nitrogen and phosphorus on algae growth in actual water body are very complex.Different ratios of nitrogen to phosphorus,the existing forms and spatial distribution of nitrogen and phosphorus,the release of nutrients from sediment,the types of land use near the water source area and the input of exogenous pollutants are all key factors affecting algae growth[2,40,51]。
Carbon source is an essential element for the growth of algae.Hydroxide,bicarbonate and CO2in water form a carbonate system,in which CO2and bicarbonate are the main carbon sources used by algae.The composition of the carbonate system determines the availability of carbon sources for algae,and the assimilation of carbon sources by algae will also shift the equilibrium of the carbonate system,resulting in the increase of pH value[52]。
Trace elements such as iron,manganese and copper,although their concentrations are far lower than those of carbon,hydrogen,oxygen and other macroelements,can participate in various biochemical reactions as cofactors[53]。 The effect of trace elements is related to the existing form of the element,the pH value of the water environment and other factors,and too high concentration may produce toxicity and inhibit the growth of algae.Taking copper ion as an example,when the pH value was 6,the median effective concentration（EC50）of extracellular soluble Cu2+for inhibiting the growth of Chlorella vulgaris was 30μg/L,and when the pH value increased to 7.5,the value decreased to 1.1μg/L[54]。
Dissolved oxygen(DO)is also a factor closely related to the growth of algae.While algae produce oxygen through photosynthesis,the respiration of algae and other aquatic organisms also consumes oxygen.DO in water is also affected by temperature,air pressure and other factors.Therefore,the current research on algae and DO is more correlation analysis than causal inference.the correlation between algae and DO is not consistent in different literature reports.For example,when Wang et al constructed the niche model of Microcystis in Chaohu Lake,they found that there was a significant positive correlation between DO and Microcystis biomass through redundancy analysis[55]。 Swanepoel et al.Reported the opposite result when they constructed a Microcystis concentration model for the Vaal Dam in South Africa[56]。 Considering the growth characteristics of algae,it may be more practical to infer the future bloom state according to the difference of dissolved oxygenΔDO between day and night in practical application。

2.3 Biological factor

Biological factors mainly include algae species and other aquatic organisms that can interact with algae,such as zooplankton,submerged plants,herbivorous fish,bacteria,etc。
the dominant algal species in eutrophic water is an important factor affecting the scale and outbreak characteristics of algal blooms.algae species in the water source area of lakes and reservoirs belong to freshwater algae species,which can be divided into planktonic algae and attached algae according to their niches,among which planktonic algae are the main group leading to water blooms in the water source area[57]。 the community structure of phytoplankton is diverse,and cyanobacteria,green algae and diatoms are the most widely distributed and the largest number of species in freshwater lakes and reservoirs in China.Seasonal factors,lake and reservoir eutrophication,and ecosystem complexity all affect the composition of dominant species.Although there are many species of green algae,they are not always dominant species,especially in lakes and reservoirs with high eutrophication,cyanobacteria often become dominant species throughout the year because of their competitive advantages in carbon,nitrogen,and light conditions[58]。 Algae species also release allelopathic compounds to interfere with the growth of competitors,thus gaining an advantage in the competition for scarce resources[59]。
submerged plants are usually the victims of water blooms,but some studies have shown that Submerged plants can effectively inhibit the growth of phytoplankton,improve water transparency and improve water quality in mesotrophic to eutrophic water[60]。 Zooplankton and herbivorous fish,as predators of algae in aquatic ecosystems,play an important role in maintaining the balance of aquatic ecology and contribute to the ultimate reduction of algae biomass[61,62]。 bacteria can decompose organic matter to produce nutrients and play an important role in the material cycle,which may promote the outbreak of water blooms.Moreover,by storing and recycling nutrients,Bacteria may change the limiting nutrient factors of phytoplankton,thereby affecting the chemical composition of algae[63]。

3 Algae concentration prediction model

the biomass of algae in water body is a multivariate nonlinear function of many influencing factors.If the functional relationship can be approximately described by a suitable mathematical model,the prediction model of algae concentration can be constructed,and then the risk of algal bloom outbreak can be assessed.At present,algae prediction models can be divided into two categories,namely,Process-based models and Data-driven models[64]。 the former constructs mathematical models with causality by studying and quantifying physicochemical,biochemical mechanisms and kinetic processes.the latter identifies the patterns and rules in the monitoring data through data analysis,mining and statistical methods,and constructs the optimal correspondence rules between the input parameters and the output results。
Although there are many factors affecting algae growth,due to the limitation of data availability and accuracy,as well as different modeling ideas and emphases,only some of the influencing factors will be selectively used as model inputs In modeling,whether it is a process mechanism model or a data-driven model.Water temperature,nitrogen and phosphorus concentrations,and meteorological and hydraulic conditions were the most common inputs.in a large number of modeling attempts,only models that fit the actual data well and can solve practical problems will be retained。

3.1 Process mechanism model

A complete process mechanism model is usually composed of multiple sub-modules.Taking the development of Taihu lake model as an example,since the 1980s,Taihu Lake model has gone through three stages of development.the initial process mechanism model is a two-dimensional or three-dimensional hydrodynamic model,which emphasizes the influence of current,wind and wave,that is,the role of physical factors.Subsequently,the role of chemical impact factors was taken into account,the mass transport and mass cycle processes were introduced,and the spatial distribution of nutrients and the precipitation and resuspension of particulate matter were included in the model.Furthermore,a relatively complete ecological model was formed by combining biological processes with Lake hydrodynamics and hydrochemistry,and considering the interaction between macrophytes,zooplankton and phytoplankton[65]。 the water quality prediction model constructed by Hamilton et al.For Prospect reservoir in Australia also includes a hydrodynamic module,a particulate matter module,and an aquatic ecology module,which are respectively used to describe the one-dimensional vertical distribution of temperature and salinity in the Reservoir,the sedimentation,aggregation,and diffusion of particulate matter,the growth dynamics of phytoplankton,and the biochemical reactions of other water quality components[66,67]。
Based on the above studies,it can be seen that the lake process mechanism model is a combination of the hydrodynamic model,the water quality model,and the aquatic ecological model.Figure 2 describes the modeling framework of the process mechanism model.Among them,the hydrodynamic model and water quality model are relatively perfect,and have been applied to various commercial software such as MIKE,CE-QUAL-W2 and HEC-RAS.algae growth model is the core of aquatic ecological model.Due to the complexity of biochemical processes and the site-specific parameters,the current research is still immature,and the simulation effect of the actual Algae growth process is limited。
图2 过程机理模型框架

Fig. 2 Process-based models framework

the optimization of algae growth model has always been The focus of model development.The change of algal biomass in water is determined by both the growth and decay of algae[68,69]。 The growth term includes The environmental conditions required for algae growth,such as water temperature,light,nutrient(mainly including nitrogen and phosphorus)concentration,etc;The attenuation term usually includes algae respiration,algae death,aquatic animal predation,and algae sedimentation,and some models combine algae respiration and death into one term[70]。
Based on the exploration experiments of a large number of factors affecting the growth of algae,the dynamic equation describing the growth term has been widely and maturely studied,and its expression usually takes the Monod equation as the core framework and embeds the response function of algae cells to specific factors such as temperature,light,nutrients and so on.Although there are systematic theoretical and experimental evidences for the attenuation of algae,there are few quantitative studies on the dynamics[71]。 Therefore,the expression of the attenuation term related equation in the existing model is also relatively simple.algal respiration is quantified in terms of respiration rate,which is usually defined as a univariate function of water temperature.Algae settling is described by a settling rate,usually expressed as an empirical constant or as a function of water depth.Algal mortality is described by the specific mortality rate,which is expressed as an empirical constant in most growth mechanism models,and is regarded as a function of Algal biomass in a few models[68]。 in most cases,the predation of aquatic animals lacks raw data and is usually ignored In the actual modeling process。
Table 1 summarizes the model kinetic equations related to algae growth reported in some literatures and evaluates the application effect of the corresponding models.Table 2 summarizes the meanings of the parameters involved in the listed models and the corresponding symbols。
表1 Kinetic Equations for Growth and Decay of Algae

Table 1 Kinetic equations of algae growth and decay

NO. Model content Model evaluation Ref
1 Growth kinetic equation: ∂CA/∂t=(RG-RD-Q/V)·CA-Graz·Z
Algae growth: RG=μmax·f(T)·f(I)·f(TN)·f(TP)
① Temperature response: f(T)=exp[-(2.3|T-Topt|)/15]
② Light response: f(I)=I/(I+KI)
③ Nutrients response: f(TN)=TN/(TN+KN); f(TP)=TP/(TP+KP)
Algae decay
⑤ Cell death: RD=Mmax·e(2.3/15.0)(Topt-T)·CA/(CA+KM)·KP/(TP+KP)T≤Topt;
RD=Mmax·CA/(CA+KM)·KP/(TP+KP)T>Topt
⑥ Aquatic organisms predation: Graz=Gmax·CA/(CA+KZ)		 The simulation results of each sampling point in Taihu Lake
showed that the model had good stability and the simulated
values could fit the measured values well, but the fitting effect
had not been evaluated quantitatively. The growth model parameters measured in the laboratory might differ from that in actual environment, which resulted in the error between the simulated values and measured values.		 68
2 Growth kinetic equation: ∂CA/∂t=(RG-RD-S)·CA
Algae growth: RG=μmax·f(I)·f(T)·f(NP)
① Temperature response: f(T)=1-(T-Topt)2/(Topt)2
② Light response: f(I)=I/Iopt·exp(1-I/Iopt)
③ Nutrients response: f(NP)=min[TP/(KP+TP),TN/(KN+TN)]
Algae decay: RD=R+M
④ Respiratory metabolism: R=kR·θRT-20
⑤ Cell death: M=kM
⑦ Algae Settlement: S=vS/H		 The results showed temperature and total phosphorus were the primary factors influencing algae growth in Taihu Lake. The research did not involve the fitting effect of the model to the actual data, but rather aimed to explore the main factors affecting the algae growth in Taihu Lake through the sensitivity analysis of model parameters.
 50
3 Growth kinetic equation: ∂CA/∂t=(RG-RD-S)·CA
Algae growth: RG=μmax·f(T)·f(I)·f(TN)·f(TP)
① Temperature response: f(T)=θGT-20
② Light response: f(I)=I/(KI+I)
③ Nutrients response: f(TN)=TN/(KN+TN); f(TP)=TP/(KP+TP)
Algae decay: RD=R+M
④ Respiratory metabolism: R=kR·θRT-20
⑤ Cell death: M=kM
⑦ Algae Settlement: S=vS/H		 The model's predicted value aligned well with the measured data, with an average relative error of less than 20%. This suggested that the model could accurately reflect the dynamic growth of algae to a certain extent. The model showed potential for predicting algal blooms in shallow and temperate lake systems. 70
4 Growth kinetic equation
∂CA/∂t={μmax·min[f(TP):f(TN):f(I)-R-M]f(T)·CA-Kraz·fraz(T)Z·fraz(CA)·CA
① Temperature response: f(T)=θR T-20
② Light response: f(I)=(I/Iopt)·e(1-I/Iopt)
③ Nutrients response: f(TP)=(TP-TPmin)/(TPmax-TPmin);
f(TN)=(TN-TNmin)/(TNmax-TNmin)
④ Respiratory metabolism: R=kR
⑤ Cell death: M=kM
⑥ Aquatic organisms predation: Graz=Kraz·fraz(T)·Zfraz(CA)·TP;
fraz(CA)= CA/(KZ+ CA); fraz(T)=θrazT-20		 The one-dimensional Water quality model (DYRESM Water Quality) combined hydrodynamics and ecological process models to simulate water quality. The core equations of the ecological process components were phytoplankton growth and nutrient cycling. Simulation results for chlorophyll a indicate an average error of 24.1% and a standard deviation of 19.7% when compared to measured values. 66,67
表2 Summary of model parameters

Table 2 Summary of model parameters

Meaning Unit Symbol Meaning Unit Symbol
Algae biomass mg/L CA Optimum growth temperature ℃ Topt
Specific growth rate d-1 RG Light intensity half-saturation coefficient μE/(m2∙s) KI
Specific decay rate d-1 RD Optimal light intensity μE/(m2∙s) Iopt
Aquatic animal biomass mg/L Z Total nitrogen half-saturation coefficient mg/L KN
Predation rate d-1 Graz Total phosphorus half-saturation coefficient mg/L KP
Respiratory metabolic rate d-1 R Maximum mortality d-1 Mmax
Mortality d-1 M Mortality half-saturation coefficient mg/L KM
Settlement rate d-1 S Maximum predation rate d-1 Gmax
Water temperature ℃ T Predation half-saturation coefficient mg/L KZ
Light intensity μE/(m2∙s) I Respiration rate d-1 kR
Total nitrogen concentration mg/L TN Temperature influence coefficient on respiration 1 θR
Total phosphorus concentration mg/L TP Constant mortality d-1 kM
Lake reservoir discharge m3/d Q Constant settlement rate m/d vS
Lake reservoir area m2 V Temperature influence coefficient on growth 1 θG
Water depth m H Aquatic predation rate constant 1 Kraz
Maximum specific growth rate d-1 μmax Temperature influence coefficient on predation d-1 θraz
As a forward derivation model,the process mechanism model emphasizes causal inference,so the perfect process mechanism model has good interpretability and generalization ability,and has been widely used in recent years.For example,Elliott et al.combined the phytoplankton community model PROTECH with the Lake physical model PROBE to simulate the phytoplankton community in lake Erken,Sweden,and the simulation results of diatoms and cyanobacteria were better[72]。 Patynen et al.Combined the phytoplankton community model PROTECH with the one-dimensional hydrodynamic model Mylake to test the potential impact of climate warming on phytoplankton in Pyhajarvi Lake,Finland,and pointed out that climate warming may advance the time of diatom outbreak in spring[73]; Based on the lake water quality model SALMO,Chen et al simulated and verified the five-year monitoring data of Meiliang Bay in Taihu lake,and pointed out that the increase of algae biomass caused by the increase of water temperature and the potential threat of climate change to the lake ecosystem[74]。
Although the process mechanism model is based on objective mechanism and experimental evidence,it can only approximate the natural phenomena such as algae growth and outbreak,and can not be accurately quantified.the existing models simplify the actual process and contain a large number of empirical formulas.Taking the Monod equation as an example,it belongs to the empirical model.Although many scholars have confirmed the rationality of the form of the Monod equation through theoretical derivation,these derivations are based on specific assumptions[75]。 the parameter calibration of the model is also a major problem at present.Xiao et al.Have shown that laboratory research simplifies complex natural conditions,making it impossible to accurately observe the key physiological processes of algae in laboratory culture.Therefore,the results of laboratory calibration parameters can not be directly transferred to the actual water body,and more accurate calibration needs to be carried out through pilot or field tests,which is rarely carried out at present[76]。
the process mechanism model can not expect to improve the performance by increasing the complexity of the model.the more complex the structure of the model is,the more requirements for monitoring environmental factors will be,and the cost of model construction will be increased accordingly.Due to the limitation of environmental monitoring data,many natural process parameters can not be observed and obtained,and some structures of the model need to be adjusted or simplified in practical application,resulting in limited prediction performance[77]。

3.2 Data driven model

the goal of data-driven model is to construct the optimal mathematical correspondence between output indicators and input indicators,which belongs to the"black box"model.Compared with the process mechanism model,the data-driven model focuses on feature factor identification and data rule mining,and trains the"black box"through a large number of training set data in order to achieve good prediction results on the test set data.the construction of data-driven model is inseparable From the development and optimization of machine learning algorithms,which are rapidly promoted and applied in various fields in the era of big data with the rapid development of computer performance.from the most basic regression algorithm to genetic algorithm and artificial neural network,it has surpassed the process mechanism model in recent years and become the most important method to build algae prediction model at this stage[64]。 Figure 3 depicts the modeling framework of the data-driven model。
图3 数据驱动模型框架

Fig. 3 Data-driven models framework

regression algorithm is the most common method of data-driven model construction,among which multiple linear regression method is widely used because of its low threshold and intuitive conclusion.Chen Yuwei et al.Constructed a multiple regression model between cyanobacteria and environmental factors in Meiliang Bay of Taihu Lake,and identified significant correlation factors[78]。 Based on the historical monitoring data of Yeongsan Reservoir in Korea,Cho et al.Established four multiple linear regression and principal component regression models for the prediction of chlorophyll a concentration,and compared the performance of different models[79]。 Based on the data of 494 lakes in Central and Northern Europe,Richardson et al.Assessed the response of cyanobacteria to lake nutrients,water temperature,hydraulic retention time and other factors through multiple linear regression analysis,and pointed out that the response of cyanobacteria community to environmental conditions was site-specific[80]。
linear correlation analysis and linear regression methods can construct concise models and get intuitive conclusions,but they are not suitable for describing nonlinear processes in nature,so they need to be further extended on the basis of linear regression.Hu et al.Constructed a binary logistic regression model to calculate the outbreak probability of blue-green algae blooms in the outer sea of Dianchi Lake,and the results showed that water temperature had a strong positive impact on the outbreak probability,while other water quality factors had no significant impact[81]。 Huo et al.Constructed a generalized additive nonlinear regression model based on the data of 26 lakes and reservoirs in China from 1996 to 2005,and determined the trophic standard of lakes and reservoirs[82]。 Regression analysis can also be optimized by introducing algorithms with nonlinear relationship,such as decision tree and random forest algorithms,support vector machine algorithms,etc[83]。 In addition,the autoregressive model based on time series analysis has attracted attention because it reduces the input indicators,reduces the uncertainty of the model and the cost of monitoring.Chen et al.Established a short-term prediction model of chlorophyll-a concentration by using ARIMA method,and Xiao et al.Established a prediction model of algal bloom by combining wavelet analysis and artificial neural network.Both of them have achieved effective prediction and early warning of algal blooms through a single parameter,but they have not been further promoted because they can not explain the internal and external mechanisms of algal blooms and are only applicable to eutrophic water bodies at present[84][85]。
Genetic algorithm is based on Darwin's principle of natural selection,which searches for the optimal solution by simulating the process of natural evolution,and is a commonly Used optimization algorithm in modeling.Recknagel et al.used the hybrid evolutionary algorithm HEA to construct an early warning model for cyanobacteria and microcystins in reservoirs in Australia and South Africa[86]。 genetic algorithms are also commonly used in combination with other intelligent methods for optimization.Wang et al.Combined Genetic algorithm with BP neural network and least squares support vector machine algorithm to improve the model accuracy and generalization ability[87]。
artificial neural network algorithm is one of the current hot research fields,which is characterized by its ability to simulate the activities of the human brain,learn patterns and relationships from complex data,and thus achieve regression or prediction.as early As the end of the last century,Artificial neural network has been applied to the prediction of algae biomass because of its ability to adapt to the complexity and nonlinearity of ecological phenomena,and it is still an important method in the study of algal blooms and has been continuously optimized[88]。 For example,Kim et al.Optimized the input variables and neural network structure to improve the interpretability of the model by incorporating the ecological mechanism into the deep learning model[89]。
in recent years,some scholars regard remote sensing prediction model,process mechanism model and data-driven model as the third type of algal bloom prediction model.remote sensing technology is a means of data monitoring and acquisition,which extracts water quality information through photothermal sensors carried by satellites and aircraft.Its characteristics are that it can obtain multi-site and high-frequency remote sensing data.the establishment of prediction models requires the processing and analysis of remote sensing data,and In fact,data-driven methods are still the main methods.For example,cyanobacterial blooms can be predicted by empirical or semi-analytical models based on cyanobacterial data obtained from the absorption characteristics of chlorophyll and phycocyanin at 670 nm and 620 nm,respectively[90]。 Due to the limitation of instrument resolution,remote sensing models are usually suitable For large-scale water bodies such as large lakes or oceans.for example,Dippner et al.Constructed a prediction model of harmful algae blooms in the coastal upwelling area of Vietnam by combining satellite images and field observations,which well predicted the drift and diffusion of harmful algae blooms during the southwest monsoon[91]。 Pierson et al.Developed a semi-analytical model for lake Malaren(the third largest Lake in Sweden)that accurately evaluates the brightness reflectance spectrum as a function of the concentration of optically active substances,thereby retrieving the concentration of chlorophyll-a in the water from the underwater reflectance in remote sensing data[92]。 It is worth mentioning that although chlorophyll a is often used as an indicator of the number of algae cells in remote sensing prediction models,due to the diversity of algae species,chlorophyll a does not correspond to the size of algae cells and specific species.different algae species contain different pigment contents and types,and their light absorption and reflection spectra are different,showing different colors,which provides a basis For remote sensing to monitor specific algae blooms.for example,Shen et al.Proposed a method based on the slope of the green-red spectrum to identify the dominant species in diatom and dinoflagellate blooms[93][94]。
Table 3 summarizes the algae prediction models constructed by data-driven method reported in some literatures,including modeling method,model content and model evaluation。
表3 Algae prediction model based on data-driven method

Table 3 Algae prediction models based on data-driven methods reported

Modeling method Model content and evaluation Ref
Multiple stepwise
regression		 · The standardized regression equation was: ln(TB+1)=1.16×ln(WT+1)+5.4×ln(TP+1)-2.33. In this equation, TB represented the total algae biomass, WT represented the water temperature, and TP represented the total phosphorus.
· The correlation coefficient for the prediction model of total algae biomass was 0.65, indicating a significant correlation.
· During the high algal phase in summer, the model was unable to simulate the effects of wind waves and lake currents, resulting in a significant discrepancy between the predicted and measured values.		 78
Binary logistic
regression model		 · The log-likelihood function was: ln L(α,β)=∑ni=1[yi(α+β’Xi)-ln(1+eα+β’Xi)]
· The model's predicted probability closely matched the outbreak frequency between April and October, but was slightly lower during January to March and November to December. The trends remained consistent.
· The model was imprecise when the lake was heterogeneous and not well-mixed, and it neglected information on the intensity of the bloom outbreak.		 81
Generalized additive
Models (GAMs)		 · Construct generalized additive models to determine the nutrient standard. Use chlorophyll a as the response variable and total nitrogen, total phosphorus and monthly average surface air temperature as the explanatory variables.
· The model parameters were found to be significant (p < 0.001), and the AIC and GCV results indicated appropriate explanatory variables.
· The results indicated that an increase in water temperature would significantly decrease the nutrient standard values. It was recommended to strictly control the total phosphorus to suppress algal blooms.		 82
Autoregressive
Integrated Moving
Average Model
(ARIMA)		 · An autoregressive integrated moving average (ARIMA) model was established for the daily concentration of chlorophyll a, and compared with a multivariate linear regression (MVLR) model.
· The MVLR model required several inputs, while the ARIMA model only required one input variable. However, the ARIMA model might not provide a clear understanding of the mechanisms that affect algal blooms.
· The Index of Agreement (IoA) for the ARIMA model was 0.86, significantly higher than that of the MVLR model (0.55), indicating greater potential for early warning applications.		 84
Wavelet analysis
combined with artificial
neural network (ANN)		 · A single-parameter wavelet neural network (WNN) approach was constructed to predict harmful algal blooms (HAB). The approach demonstrated high accuracy in predicting HAB in both a lake and a reservoir.
· Compared to ARIMA and ANN models, the WNN model performed better with an R value of up to 0.986 and an average absolute error as low as 0.103×104 cells/mL.
· Reliable and precise forecasts required daily data on cell density or chl a, which might be impractical for some applications due to limited budgets.		 85
Hybrid Evolutionary
Algorithm (HEA)		 · Inferential models using the hybrid evolutionary algorithm (HEA) were developed to achieve a 10- to 30-day-ahead prediction on concentrations of cyanobacteria cells or cyanotoxins.
· Model performance R2 ranged from 0.3 to 0.7 depending on the output index (cells or microcystins), study site, prediction time and validation methods.		 86
the advantage of data-driven model is that the requirements for professional domain knowledge are relatively relaxed.When the amount of training data is sufficient,the model can often have good performance by optimizing the algorithm or adjusting the model structure.However,as a"black box"model,its interpretability is relatively limited,and it is difficult to explain the process and driving factors of bloom formation,so it may take the outcome variables caused by algae growth as the driving factors of algae growth,and get the results that deviate from the natural process mechanism[48]。 in addition,the algae prediction model based on the data-driven method is also linked to the training data of a specific water body,and the model constructed with the same algorithm In different water sources may be completely different。

3.3 Comparison of process mechanism model and data-driven model

There is no difference between the two types of modeling methods,which need to be flexibly chosen according to the research problems,the data available,the decision-making or management needs。
the equations of the process mechanism model have clear physical meaning,which is helpful to identify the nature of the algal bloom problem and formulate countermeasures.However,it is often impossible to achieve good prediction results only by algae growth models,and it is necessary to combine with hydrodynamics and water quality models to form a more complete comprehensive model.the complete process mechanism model has good stability and universality,and the simulation and prediction results of different water systems are reliable,but it involves many natural processes and contains a large number of unknown parameters,so the workload of data monitoring and model calibration is huge.In addition,the model is also an approximate estimation for the quantification of natural processes,and some biochemical processes are not yet clear,so there are inevitably systematic errors。
data-driven model attaches great importance to data mining and analysis,and its modeling methods are diverse and do not depend On professional knowledge.on the basis of the current high computing performance of computers,the modeling cycle is short.However,the interpretability of the model is poor,and most of the parameters only have mathematical meaning.the model is usually closely related to the state of the system under study.When the external conditions of the system change or migrate to another system,the reliability of the model may be significantly reduced.Therefore,the data-driven model is more suitable for the study of problems in a specific area with a short time span,and in order to maintain the performance of the model,it is necessary to iteratively optimize the model parameters with the latest data。
Table 4 lists the strengths and weaknesses of the process mechanism model and the data-driven model.Both types of models require a large amount of data to train the model.the dimension and volume of the data that can be obtained determine the upper limit of the model performance.the selection and optimization of modeling methods can improve the lower limit of the model performance.Compared with the process mechanism model,the data-driven model is more flexible and diverse,and the model structure is relatively simple,so it is the preferred modeling method In most of the current research.in order to make full use of the interpretability of process mechanism and the data mining ability of data-driven methods,algae growth mechanism and artificial intelligence methods can be combined to improve the applicability and effectiveness of the model and reduce the cost of modeling.For example,Wang et al.determined the characterization index of algae density and the main factors affecting algae reproduction by analyzing the chemical mechanism of algae growth and photosynthesis process,improved the accuracy of algae growth description and screened the input index of prediction model[87]。 Wang Xiaoyi et al.Constructed a growth mechanism model and a cusp catastrophe model respectively to simulate the formation and outbreak of cyanobacteria blooms in lakes and reservoirs,and used genetic algorithm to optimize the parameters in the model,and finally formed a comprehensive model,which overcame the defects of a single mechanism model and improved the prediction accuracy of the model[95]。
表4 Comparison of Process Mechanism Model and Data Driven Model

Table 4 Comparison between process-based models and data-driven models

Process-Based models Data-Driven models
Advantage 1. Good interpretability and generalization ability.
2. Identify the bloom triggers and assist in decision and management.		 1. The model performs better on specific problems.
2. Do not rely on professional knowledge
3. Modeling methods are diverse and flexible.
Disadvantage 1. Many unknown parameters require experimental calibration.
2. The mechanisms behind part of the processes are still unclear.
3. Huge modeling cost and high application threshold.		 1. Lack interpretability and generalization and have the risks of falling into local optimality and overfitting.
2. Usually only applicable to specific data and regions.
3. The model structure and parameters need to be adjusted according to the system status changes.
Similarity 1. Rely on monitoring data. Models cannot be built without sample data.
2. The appropriate method should be selected according to the modeling conditions and objectives.
3. There is a general trend to combine knowledge of process mechanisms with data mining and analysis methods.

4 Conclusion and prospect

According to the impact factors of algae growth and a large number of existing research reports on algae concentration prediction models,the summary is as follows:
(1)Among many factors,water temperature and nitrogen and phosphorus concentration are usually the key factors affecting algae growth,and are also the most common input indicators of the model,followed by meteorological indicators such as light and rainfall.Biological factors are usually limited to theoretical analysis due to the difficulty of data acquisition,and are rarely included in the practical application of the model.In the context of global climate change,more and more attention has been paid to the impact of elevated atmospheric CO2concentrations on algae growth.In addition,the concentration of chlorophyll a is often used as a characterization of algae concentration 。
(2)to construct the algae concentration prediction model,we should first clarify the research problems and modeling objectives,and select the appropriate method according to the available data.Generally speaking,it is more accurate to select the data-driven method For short-term forecasting,while it is more reasonable to select the process mechanism method for scenario simulation or long-term forecasting.for the water supply sector,the dynamics and concentration of algae in the high temperature season in summer and autumn deserve more attention,so more attention should be paid to the data of high algae period in the model construction。
(3)Data-driven model is becoming the mainstream method of modeling because of its flexible modeling method,good simulation effect and outstanding cost-effectiveness,but the model is specific and targeted,and usually does not have good interpretability and generalization ability.the process mechanism model is interpretable and general,but the model structure is complex,the modeling cost is high,and the simulation effect of a single algae growth model is limited,so it is rarely used alone at present。
(4)modeling can not be separated from the support of original training data.the water quality of water source and the volume and quality of meteorological data not only affect the choice of Modeling methods,but also affect the calibration of model parameters and the uncertainty of model output.At present,the model with few but precise input parameters and simple data monitoring requirements has greater application potential,while the model with complex model structure and various data monitoring indicators is difficult to promote because of its high threshold of use。
It is worth noting that the outbreak of algal blooms is not only a large increase in algae concentration,but also includes the process of algae cell aggregation,floating and migration.management should use the prediction model as an assistance tool to judge the risk of water bloom by predicting the trend of algae growth,and formulate emergency Management plans and measures in advance,so as to cope with the water supply crisis.Based on the current challenges in algae concentration prediction and bloom early warning research,the following suggestions are made for future research:
(1)Pay attention to the quality of water quality and meteorological data related to algae,and increase the frequency of data monitoring.At present,the data sets related to algae in lakes and reservoirs in China still need to be improved,and it is difficult to build an accurate and effective algae concentration prediction model For many water sources due to the lack of monitoring data or poor data quality.for the water source management department,the input data of the algae prediction model will become a long-term monitoring index to ensure that the model can operate within a certain time range.Therefore,on the basis of identifying and screening core monitoring indicators,it is necessary to increase investment in data monitoring,increase data monitoring sites,and improve the frequency and quality of data monitoring。
(2)Identify needs and objectives,analyze data availability,evaluate management costs,and select appropriate modeling methods.the process mechanism model and the data-driven model have different characteristics and application scope.Before starting the modeling,the project requirements and modeling objectives should be clarified,and the appropriate method should be selected according to the characteristics of the data to ensure the pertinence and applicability of the model.in the current era of big data,the rapid popularization and application of artificial intelligence methods make data-driven models become the mainstream.In order to build an interpretable"black box"model,the knowledge of water quality and aquatic ecology In the process mechanism model can be integrated into the feature engineering of data-driven models to simplify the input indicators of the model.For the process mechanism model,the data-driven method can also be used to optimize the model parameters and improve the model performance。

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
Zhang Y L, Deng J M, Qin B Q, Zhu G W, Zhang Y J, Jeppesen E, Tong Y D. Fundam. Res., 2023, 3(2): 265.

[2]
Smith V H. Environ. Sci. Pollut. Res., 2003, 10(2): 126.

[3]
Hu M Q, Ma R H, Xiong J F, Wang M H, Cao Z G, Xue K. Remote. Sens. Environ., 2022, 277: 113057.

[4]
Ho J C, Michalak A M, Pahlevan N. Nature, 2019, 574(7780): 667.

[5]
Huisman J, Codd G A, Paerl H W, Ibelings B W, Verspagen J M H, Visser P M. Nat. Rev. Microbiol., 2018, 16(8): 471.

[6]
Wang S Q, Zhang X, Wang C, Chen N C. Water Res., 2023, 228: 119367.

[7]
Paerl H W, Gardner W S, Havens K E, Joyner A R, McCarthy M J, Newell S E, Qin B Q, Scott J T. Harmful Algae, 2016, 54: 213.

[8]
Al-Ghussain L. Environ. Prog. Sustain. Energy, 2019, 38(1): 13.

[9]
Osman A I, Hefny M, Abdel Maksoud M I A, Elgarahy A M, Rooney D W. Environ. Chem. Lett., 2021, 19(2): 797.

[10]
Liu W, Qiu R L. J. Chem. Technol. Biotechnol., 2007, 82(9): 781.

[11]
Richardson C J, King R S, Qian S S, Vaithiyanathan P, Qualls R G, Stow C A. Environ. Sci. Technol., 2007, 41(23): 8084.

[12]
O’Neil J M, Davis T W, Burford M A, Gobler C J. Harmful Algae, 2012, 14: 313.

[13]
Paerl H W, Otten T G. Microb. Ecol., 2013, 65(4): 995.

[14]
Jardine S L, Fisher M C, Moore S K, Samhouri J F. Ecol. Econ., 2020, 176: 106691.

[15]
Pivokonsky M, Naceradska J, Kopecka I, Baresova M, Jefferson B, Li X, Henderson R K. Crit. Rev. Environ. Sci. Technol., 2016, 46(4): 291.

[16]
Li L, Gao N Y, Deng Y, Yao J J, Zhang K J. Water Res., 2012, 46(4): 1233.

[17]
Zhou S Q, Zhu S M, Shao Y S, Gao N Y. Water Res., 2015, 72: 381.

[18]
Hua L C, Lin J L, Chen P C, Huang C. Chem. Eng. J., 2017, 328: 1022.

[19]
Bei E, Li X, Wu F H, Li S X, He X S, Wang Y F, Qiu Y, Wang Y, Wang C K, Wang J, Zhang X J, Chen C. Water Res., 2020, 183: 116055.

[20]
Bei E, Ye Z W, Chen X L, Li X, Wang J, Qiu Y, Xie S G, Chen C. Sci. Total Environ., 2023, 874: 162469.

[21]
He X X, Liu Y L, Conklin A, Westrick J, Weavers L K, Dionysiou D D, Lenhart J J, Mouser P J, Szlag D, Walker H W. Harmful Algae, 2016, 54: 174.

[22]
Davis T W, Berry D L, Boyer G L, Gobler C J. Harmful Algae, 2009, 8(5): 715.

[23]
Su M, Suruzzaman M, Zhu Y P, Lu J P, Yu J W, Zhang Y, Yang M. J. Environ. Sci., 2021, 110: 119.

[24]
Li X, Wang J, Zhang X J, Chen, C. J. Environ. Sci., 2015, 32: 15.

[25]
Devi A, Chiu Y T, Hsueh H T, Lin T F. Water Res., 2021, 188: 116478.

[26]
Su M, Yu J W, Zhang J Z, Chen H, An W, Vogt R D, Andersen T, Jia D M, Wang J S, Yang M. Water Res., 2015, 68: 444.

[27]
Zhang Y. Technical guidance manual for emergency water purification of urban water supply system. 2nd ed. Beijing: China Architecture & Building Press, 2017.

(张悦. 城市供水系统应急净水技术指导手册. 第2版. 北京: 中国建筑工业出版社, 2017.).

[28]
Qin B Q, Zhu G W, Gao G, Zhang Y L, Li W, Paerl H W, Carmichael W W. Environ. Manag., 2010, 45(1): 105.

[29]
Zhang X J, Chen C, Ding J Q, Hou A X, Li Y, Niu Z B, Su X Y, Xu Y J, Laws E A. J. Hazard. Mater., 2010, 182(1-3): 130.

[30]
Cen C, Zhang K J, Zhang T Q, Zhou X Y, Pan R J. Appl. Microbiol. Biotechnol., 2020, 104(21): 9079.

[31]
Li X, Wang J, Liu Y Y, Shi J, Zhang X J, Chen C. J. Water Supply Res. Technol. Aqua, 2015, 64(7): 847.

[32]
Brooks B W, Lazorchak J M, Howard M D A, Johnson M V V, Morton S L, Perkins D A K, Reavie E D, Scott G I, Smith S A, Steevens J A. Environ. Toxicol. Chem., 2016, 35(1): 6.

[33]
Bei E, Wu X M, Qiu Y, Chen C, Zhang X J. Acc. Chem. Res., 2019, 52(4): 867.

[34]
Liu X M, Zhang G X. Advances in Water Science, 2022, 33(02): 316.

(刘雪梅, 章光新. 水科学进展, 2022, 33(02): 316.)

[35]
Lürling M, Eshetu F, Faassen E J, Kosten S, Huszar V L M. Freshw. Biol., 2013, 58(3): 552.

[36]
Paerl H W. Life-Basel, 2014, 4(4): 988.

[37]
Ferris J M, Christian R. Aquat. Sci., 1991, 53(2): 187.

[38]
Gong C, Gong D D, Liu D F, Zhang J L, Yan G H. Research of Environmental Sciences, 2020, 33(05): 1214.

(龚川, 贡丹丹, 刘德富, 张佳磊, 严广寒. 环境科学研究, 2020, 33(05): 1214.).

[39]
Xu K, Jiang H B, Juneau P, Qiu B S. J. Appl. Phycol., 2012, 24(5): 1113.

[40]
Qin B Q, Wang X D, Tang X M, Feng S, Zhang Y L. Adv. Earth Sci., 2007, 22(9): 896.

(秦伯强, 王小冬, 汤祥明, 冯胜, 张运林. 地球科学进展, 2007, 22(9): 896.).

[41]
Yun Y S, Park J. Appl. Microbiol. Biotechnol., 2001, 55(6): 765.

[42]
Su M, Jia D M, Yu J W, Vogt R D, Wang J S, An W, Yang M. Sci. Total Environ., 2017, 574: 1477.

[43]
Jia Z Y, Su M, Liu T T, Guo Q Y, Wang Q, Burch M, Yu J W, Yang M. Harmful Algae, 2019, 88: 101658.

[44]
Liang P Y, Wang X, Ma F B. Journal of Lake Sciences, 2013, 25(04): 455.

(梁培瑜, 王烜, 马芳冰. 湖泊科学, 2013, 25(04): 455.).

[45]
Long T Y, Wu L, Meng G H, Guo W H. Ecol. Model., 2011, 222(1): 112.

[46]
D’Amours O, Scheibling R E. J. Exp. Mar. Biol. Ecol., 2007, 351(1-2): 129.

[47]
Mitrovic S M, Oliver R L, Rees C, Bowling L C, Buckney R T. Freshw. Biol., 2003, 48(1): 164.

[48]
Jones I D, Elliott J A. Freshw. Biol., 2007, 52(6): 988.

[49]
Song K Y, Zhu S F, Lu Y, Dao G H, Wu Y H, Chen Z, Wang S N, Liu J H, Zhou W G, Hu H Y. Front. Environ. Sci. Eng., 2022, 16(10): 129.

[50]
Liu Q Q, Gao Y, Xu X F. Advances in Environmental Science and Engineering, PTS 1-6(Eds. Iranpour R, Zhao J, Wang A, Yang F L, Li X). Hohhot,China, 2012, 518-523: 4961.

[51]
Xie L Q, Xie P, Li S X, Tang H J, Liu H. Water Res., 2003, 37(9): 2073.

[52]
Janka E, Umetani I, Sposob M, Bakke R. Photosynthetica, 2020, 58: 236.

[53]
Zhang X K, Li B L, Xu H, Wells M, Tefsen B, Qin B Q. Water Res., 2019, 151: 500.

[54]
De Schamphelaere K A C, Stauber J L, Wilde K L, Markich S J, Brown P L, Franklin N M, Creighton N M, Janssen C R. Environ. Sci. Technol., 2005, 39(7): 2067.

[55]
Wang Z C, Li Z J, Li D H. Chin. J. Oceanol. Limnol., 2012, 30(4): 587.

[56]
Swanepoel A, Barnard S, Recknagel F, Cao H. Water SA, 2016, 42(2): 243.

[57]
Zhang W Z, Shen H, Zhang J, Yu J, Xie P, Chen J. Chemosphere, 2020, 239: 124702.

[58]
Kong F X, Ma R H, Gao J F, Wu X D. Journal of Lake Sciences, 2009, 21(3): 314.

(孔繁翔, 马荣华, 高俊峰, 吴晓东. 湖泊科学, 2009, 21(3): 314.).

[59]
Gross E M. Crit. Rev. Plant Sci., 2003, 223-4: 313.

[60]
van Donk E, van de Bund W J. Aquat. Bot., 2002, 72(3-4): 261.

[61]
Ali Ger K, Urrutia-Cordero P, Frost P C, Hansson L A, Sarnelle O, Wilson A E, Lürling M. Harmful Algae, 2016, 54: 128.

[62]
Datta Saha S, Jana B B. J. Fish Biol., 1998, 53(1): 12.

[63]
Danger M, Oumarou C, Benest D, Lacroix G. Funct. Ecol., 2007, 21(2): 202.

[64]
Rousso B Z, Bertone E, Stewart R, Hamilton D P. Water Res., 2020, 182: 115959.

[65]
Hu W P. Ecol. Model., 2016, 319: 9.

[66]
Hamilton D P, Schladow S G. Ecol. Model., 1997, 96(1-3): 91.

[67]
Schladow S G, Hamilton D P. Ecol. Model., 1997, 96(1-3): 111.

[68]
Xu Q J, Qin B Q, Chen W M, Chen Y W, Gao G. Journal of Lake Sciences, 2001, (02): 149.

(许秋瑾, 秦伯强, 陈伟民, 陈宇炜, 高光. 湖泊科学, 2001, (02): 149.).

[69]
Bruce L C, Hamilton D, Imberger J, Gal G, Gophen M, Zohary T, Hambright K D. Ecol. Model., 2006, 193(3-4): 412.

[70]
Ding L, Wu J Q, Pang Y, Li L, Gao G, Hu D W. Ecol. Eng., 2007, 31(3): 200.

[71]
Bidle K D, Falkowski P G. Nat. Rev. Microbiol., 2004, 2(8): 643.

[72]
Elliott J A, Persson I, Thackeray S J, Blenckner T. Ecol. Model., 2007, 202(3-4): 421.

[73]
Patynen A, Elliott J A, Kiuru P, Sarvala J, Ventela A M, Jones R I. Boreal Environ. Res., 2014, 19(1): 66.

[74]
Chen Q W, Zhang C C, Recknagel F, Guo J, Blanckaert K. Ecol. Model., 2014, 273: 109.

[75]
Liu Y. Appl. Microbiol. Biotechnol., 2007, 73(6): 1241.

[76]
Xiao M, Hamilton D P, O’Brien K R, Adams M P, Willis A, Burford M A. Harmful Algae, 2020, 92: 101732.

[77]
Omlin M, Reichert P, Forster R. Ecol. Model., 2001, 1411-3: 77.

[78]
Chen Y W, Qin B Q, Gao X Y. Journal of Lake Sciences, 2001, (01): 63.

(陈宇炜, 秦伯强, 高锡云. 湖泊科学, 2001, (01): 63.).

[79]
Cho K H, Kang J H, Ki S J, Park Y, Cha S M, Kim J H. Sci. Total Environ., 2009, 407(8): 2536.

[80]
Richardson J, Miller C, Maberly S C, Taylor P, Globevnik L, Hunter P, Jeppesen E, Mischke U, Moe S J, Pasztaleniec A, Søndergaard M, Carvalho L. Glob. Change Biol., 2018, 24(11): 5044.

[81]
Sheng H, Liu H, Wang C Y, Guo H C, Liu Y, Yang Y H. Ecol. Inform., 2012, 10: 37.

[82]
Huo S L, He Z S, Ma C Z, Zhang H X, Xi B D, Xia X H, Xu Y, Wu F C. J. Hydrol., 2019, 569: 698.

[83]
Harris T D, Graham J L. Lake Reserv. Manag., 2017, 33(1): 32.

[84]
Chen Q W, Guan T S, Yun L, Li R N, Recknagel F. Harmful Algae, 2015, 43: 58.

[85]
Xiao X, He J Y, Huang H M, Miller T R, Christakos G, Reichwaldt E S, Ghadouani A, Lin S P, Xu X H, Shi J Y. Water Res., 2017, 108: 222.

[86]
Recknagel F, Orr P T, Bartkow M, Swanepoel A, Cao H Q. Harmful Algae, 2017, 69: 18.

[87]
Wang L, Wang X Y, Jin X B, Xu J P, Zhang H Y, Yu J B, Sun Q, Gao C, Wang L B. Saudi J. Biol. Sci., 2017, 24(3): 556.

[88]
Recknagel F, French M, Harkonen P, Yabunaka K I. Ecol. Model., 1997, 96(1-3): 11.

[89]
Kim T, Shin J, Lee D, Kim Y, Na E, Park J H, Lim C, Cha Y. Water Res., 2022, 215: 118289.

[90]
Sagan V, Peterson K T, Maimaitijiang M, Sidike P, Sloan J, Greeling B A, Maalouf S, Adams C. Earth Sci. Rev., 2020, 205: 103187.

[91]
Dippner J W, Nguyen-Ngoc L, Doan-Nhu H, Subramaniam A. Harmful Algae, 2011, 10(6): 606.

[92]
Pierson D C, Strömbeck N. Sci. Total Environ., 2001, 268(1-3): 171.

[93]
Rolim S B A, Veettil B K, Vieiro A P, Kessler A B, Gonzatti C. Environ. Sci. Pollut. Res., 2023, 30(8): 19602.

[94]
Shen F, Tang R G, Sun X R, Liu D Y. Remote. Sens. Environ., 2019, 235: 111484.

[95]
Wang X Y, Zhang X P, Liu Z W, Xu J P, Dong S Q. Acta Scientiae Circumstantiae, 2012, 32(07): 1677.

(王小艺, 赵载平, 刘载文, 许继平, 董硕琦. 环境科学学报, 2012, 32(07): 1677.).

Options
Outlines

/

〈 〉