image
Home Journals Progress in Chemistry
Progress in Chemistry

Abbreviation (ISO4): Prog Chem      Editor in chief: Jincai ZHAO

About  /  Aim & scope  /  Editorial board  /  Indexed  /  Contact  / 
Online first  /  Current issue  /  All issues  /  Top access  /  RSS

Progress in Chemistry >

2024 , Vol. 36 >Issue 10: 1541 - 1558

DOI: https://doi.org/10.7536/PC240215

综述

Microbubble/Droplet Manipulation Based on Marangoni Effect

  • Zhenlin Wei ,
  • Hongfei Wang ,
  • Yaliang Chen ,
  • Junbo Xing ,
  • Dayong Li , *
Expand
  • School of Electromechanical and Automotive Engineering, Yantai University, Yantai 264005, China
*e-mail:

Received date: 2024-02-22

  Revised date: 2024-07-21

  Online published: 2024-09-15

Supported by

National Natural Science Foundation of China(11972150)

Fold

Abstract

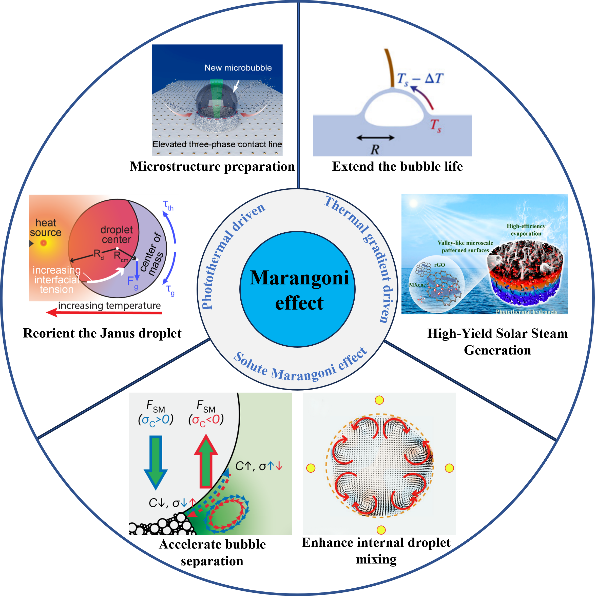
Microbubbles and microdroplets, when exposed to a uniform temperature gradient/solute concentration gradient, will undergo thermal capillary migration/solute migration, leading to the emergence of the Marangoni effect at the gas-liquid interface. This effect plays a crucial role in manipulating microbubbles or microdroplets, offering valuable applications in various fields including biology, chemistry, medicine, materials science, and micromanufacturing. In this review, provided are an overview of recent advancements about the Marangoni effect of microbubbles/droplets under different driving modes, and demonstrate the driving principle and characteristics of photothermal Marangoni effect, thermal gradient-driven Marangoni effect and solute Marangoni effect. We focus on the dynamic changes of microdroplets induced by photothermal Marangoni effect, the movement principles of droplets on diverse hydrophobic surfaces, the manipulation processes of bubble movement and bubble separation under laser irradiation, and the typical instances of bubble/droplet separation, droplet evaporation and mixing achieved through thermal gradient-driven Marangoni effect and solute Marangoni effect. Furthermore, recent applications of the Marangoni effect in microbubble/droplet manipulation are highlighted and the promising future prospects for further development and utilization of this phenomenon are discussed.

Contents

1 Introduction

2 Driving principle of the Marangoni effect

3 Temperature driven Marangoni effect

3.1 Photothermal Marangoni effect of microdroplets/ bubbles

3.2 Thermal gradient Marangoni effect of microdroplets/ bubbles

4 Microdroplet/bubble solute Marangoni effect

5 Application based on microdroplet/bubble Marangoni effect

5.1 Preparation of surface microstructure

5.2 Bubble-pen lithography

5.3 Multiphase droplet drive

5.4 Droplet motor

5.5 Emulsion energy supply

6 Conclusion and prospect

Key words： microbubble/droplet manipulation; Marangoni effect; interfacial flows; thermal gradient; concentration gradient

Cite this article

Zhenlin Wei , Hongfei Wang , Yaliang Chen , Junbo Xing , Dayong Li . Microbubble/Droplet Manipulation Based on Marangoni Effect[J]. Progress in Chemistry, 2024 , 36(10) : 1541 -1558 . DOI: 10.7536/PC240215

1 Introduction

The Marangoni phenomenon was initially discovered by James Thomson in 1855[1]. Italian physicist Carlo Marangoni studied this phenomenon for his doctoral dissertation and published the results in 1865[2], hence the phenomenon is known as the Marangoni effect. Typically, the Marangoni number Ma (a dimensionless number) is used to characterize the Marangoni effect[3]: Ma=dΔσ/Dμ, where d represents the liquid film thickness (m); Δσ represents the surface tension difference (N/m); D represents the solute diffusion coefficient (m2/s); and μ represents the dynamic viscosity of the fluid (N·s/m2). After more than a century of development, the study of the Marangoni effect has formed a complete theoretical system[4]. Figure 1 lists some important advancements in the development process of the Marangoni effect[1,2,5⇓⇓⇓⇓⇓⇓⇓⇓~14].
图1 Marangoni效应发展过程中的部分重要进展

Fig. 1 Some significant progress in the development of the Marangoni effect

As shown in Figure 1, the events from left to right are as follows: In 1855, James Thomson first discovered the Marangoni phenomenon[1]; in 1865, Carlo Marangoni published this discovery as his doctoral thesis[2]; in 1959, Young et al. first realized that Marangoni stress could control bubble movement[5]; in 1986, Ashkin et al. invented optical tweezers technology, providing a new direction for the exploration of photothermal Marangoni effects[6]; in 1990, Cazabat et al. reported on the instability of liquid film spreading driven by the Marangoni effect[7]; in 1992, Villers and Platten studied convection under the combined action of thermal capillary and thermal gravity effects in acetone[8]; in 1995, Antanovskii derived a phase-field model for the capillary phenomena of an interfacial layer formed by two incompressible liquids (applicable to flows involving topological changes in the capillary interface), obtaining a rheological expression for the reversible component of capillary stress using the free energy of a binary fluid[9]; in 2004, Saiz and Tomsia first observed images of liquid films driven by the Marangoni effect[10]; in 2013, Sempels et al. found that the Marangoni effect can reverse the coffee ring effect[11]; in 2017, Kim et al. used solute Marangoni effect to drive multiphase mixed droplets for contamination-free transport, which can be applied to clean drug delivery in the medical field[12]; in 2021, Lu et al. developed a highly efficient solar evaporator based on the Marangoni effect[13]; in 2023, Wu et al. developed a Marangoni rotor with high output speed and fuel economy, opening up new perspectives for the design of micro-rotary machinery[14].
The Marangoni effect can form Marangoni flow through the surface tension difference at the two-phase interface, thereby causing the movement, coalescence, and separation of bubbles/droplets. This characteristic demonstrates its potential for controlling bubbles/droplets[15,16]. In 1959, Young et al.[5] pioneered the use of Marangoni force to control bubble movement. Due to its non-contact nature, researchers gradually realized the significant importance of the Marangoni effect in the manipulation process of bubbles/droplets[17⇓⇓⇓⇓~22]. Currently, a series of advancements have been made in the field of micro-bubble/droplet manipulation using the Marangoni effect[23⇓⇓⇓⇓⇓⇓⇓⇓~32]. Figure 2 shows some related research and applications that utilize the Marangoni effect to achieve control over micro-bubbles/droplets, such as driving droplets on hydrophobic surfaces[33], controlling directional rotation of droplets[20], controlling particle flow around bubbles[34], inducing vortices within droplets[35], enhancing liquid flow rate in micro-scale grooves to improve solar power generation efficiency[13], and prolonging the lifespan of heated bubbles[36].
图2 不同驱动方式下Marangoni效应实现对微气泡/液滴操控的相关研究：（a）驱动疏水表面上的液滴[33]；(b）控制液滴定向旋转[20]；（c）控制气泡周围粒子流动[34]；（d）诱发液滴内部涡流[35]；（e）增强沟槽内液体流速[13]；（f）延长受热气泡寿命[36]

Fig. 2 Research on microbubble/droplet manipulation by Marangoni effect with different driving modes (a) drive droplet on the hydrophobic surface [33]; (b) control droplet rotating directionally [20]; (c) control particle flow around the bubble [34]; (d) induce vortex flow inside a droplet [35]; (e) enhance liquid flow rate in groove structure [13]; (f) extend the life of a heated bubble [36]

At the microscale, Marangoni forces have a more pronounced effect on the control of bubbles/droplets compared to convective forces and other long-range physical forces, establishing their dominant position in fields such as the manipulation, evaporation, coalescence, and separation of microbubbles/droplets[20,37⇓⇓⇓~41]. Nagelberg et al.[20] used light-induced Marangoni effects to generate Marangoni flows and net torque inside surfactant-free Janus droplets, achieving predictable and controllable reorientation of the droplets. Cira et al.[42] utilized the Marangoni effect produced by droplet evaporation to achieve spontaneous alignment, vertical oscillation, short-range pursuit, and sorting of miscible two-component droplets. Generally, the manipulation of bubbles/droplets by Marangoni effects is caused by interfacial effects due to temperature changes; for the control of droplet movement, the temperature gradient on the surface of the droplet causes a surface tension gradient, which then produces a surface shear flow from regions of lower surface tension to higher surface tension, inducing droplet motion and internal convection[43,44]. By adding light-absorbing substances inside the droplet or altering the external facilities around the droplet, the relevant manipulations can be directed towards our desired direction. For the separation and manipulation of bubbles[45], it mainly utilizes the Marangoni flow around the bubble to apply a resultant force in a certain direction, accelerating or inhibiting its detachment from the wall, thereby increasing the rate of chemical reactions[34]. Additionally, under the coupled action of buoyancy and thermal Marangoni forces, bubbles can move along with the laser, greatly expanding their application fields[47⇓⇓~50]. Next, the interfacial effect induced by changes in solute concentration, that is, due to the non-uniformity of local solute concentration, a tension gradient is generated at the interface, where the fluid flows from the region of lower surface tension to the region of higher surface tension, thus producing a solutal Marangoni effect around the bubble/droplet. Solutal Marangoni flows can be generated by the vapor drive of volatile liquids, and we can regulate the intensity of internal convection within the droplet by controlling the vapor source or changing external conditions, applying this method to mixing enhancement devices in droplet microfluidics[35].
This paper categorizes the relevant research on manipulating microbubbles/droplets based on the Marangoni effect according to the driving methods, and elaborates on the internal material exchange processes of droplets and the principles of bubble behavior control under different driving methods; it focuses on reviewing the control processes of bubbles and droplets by the photothermal Marangoni effect and the solute Marangoni effect; analyzes typical cases of bubble control by the thermal gradient Marangoni effect; introduces the practical applications of the Marangoni effect of microbubbles/droplets in various fields; and finally summarizes and prospects the challenges and potential future development directions in manipulating microbubbles/droplets using the Marangoni effect.

2 Driving Principle of the Marangoni Effect

To better illustrate the characteristics of different types of Marangoni effects in the process of bubble/droplet manipulation, this paper categorizes Marangoni effects into two types: temperature-driven Marangoni effect and solute Marangoni effect[51⇓~53], with the former further divided into photothermal Marangoni effect and thermally driven Marangoni effect based on whether a laser source is used for induction; Figure 3 illustrates the basic principles of three different driving modes of Marangoni effects. Figure 3(a) shows the principle diagram of the generation of the photothermal Marangoni effect. 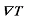Under laser irradiation, the temperature gradient ( ) produced after the droplet absorbs light energy causes a surface tension gradient (∇γ), thus inducing an internal photothermal Marangoni flow within the droplet, which flows in the opposite direction to the temperature increase. This circulating flow inside the droplet promotes mass transfer within it and alters the shape of the droplet's surface. With continuous laser irradiation, the presence of the surface tension gradient continuously affects the dynamic behavior of the droplet, causing directional movement. In applications related to bubble control using the Marangoni effect, the photothermal Marangoni effect leads to an increase in the temperature of the liquid around the bubble, thereby changing the surface tension and buoyancy of the bubble. This changes the speed at which the bubble rises or falls, ultimately affecting the stability and morphology of the bubble, triggering separation or oscillation. When the bubble oscillates in the liquid, the upward and downward Marangoni forces it experiences are 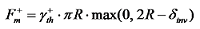, respectively. Here, represents the surface tension gradient, R represents the radius of the bubble, and 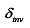represents the thickness of the inversion layer (a longitudinal temperature distribution that first increases then decreases due to the rapid cooling effect of the wall). The Marangoni force, gravity, and buoyancy collectively act on the bubble, influencing its entire oscillation process[54]. Figure 3(b) depicts the principle diagram of the thermally driven Marangoni effect. In a heated silicon oil bath, when air (at room temperature) is introduced, upon reaching the surface of the silicon oil bath, a temperature difference between the cooler top region of the bubble and the warmer bottom region of the oil bath generates an upward Marangoni effect (convection) around the bubble, making the direction of material transport opposite to gravity, which balances the forces acting on the bubble, prolonging its existence. The temperature difference-induced thermal Marangoni convection between the top and bottom of the bubble affects the overall balance of the bubble, with the development direction of the equilibrium depending on the direction of the temperature gradient. Generally, the intensity of the temperature-driven Marangoni effect is characterized by the formula Ma= 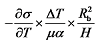, where Ma represents the Marangoni number, σ denotes surface tension (N/m); T denotes temperature (K); ΔT denotes the maximum temperature difference in the system (K); μ denotes the dynamic viscosity of the solution (N·s/m2), and α represents the thermal diffusivity of the solution (m2/s), Rb represents the bubble radius (m), and H represents the height of the liquid layer (m)[23]; the larger the Marangoni number, the stronger the Marangoni convection. Figure 3(c) illustrates the principle of the generation of the solute Marangoni effect. The blue circle on the left represents a stationary water droplet, the gray tubular shape on the right is a capillary tube (containing ethanol), and the orange area in the middle represents ethanol diffused from the capillary tube into the air. R is the radius of the droplet, and d is the distance from the droplet to the capillary tube. Since the surface tension of ethanol is lower than that of water, and the concentration of ethanol is higher in the central part of the right side of the droplet closer to the capillary tube, a flow from the center to the periphery (indicated by red arrows) occurs on the right side of the droplet. This convective phenomenon caused by the dissolution or chemical reaction of a certain component in the system is known as the solute Marangoni effect[22,55]. When a liquid film is locally thinned due to temperature or concentration disturbances, it forms a solute Marangoni flow under the action of the surface tension gradient, allowing the liquid to flow back along the optimal path to the thin liquid surface. Because the region with higher surface tension exerts a greater pull on the surrounding liquid, the liquid flows away from areas of lower surface tension. It can be seen that the solute Marangoni effect is a type of liquid flow phenomenon caused by uneven surface tension. Although the external manifestations of the three driving methods differ, fundamentally, all three arise from the presence of a surface tension gradient, meaning the liquid flows from areas of lower surface tension to areas of higher surface tension[56].
图3 3种不同Marangoni效应驱动方式的原理图：（a）液滴的激光照射区域与液滴边界区域之间的温度梯度诱导光热Marangoni效应原理图；（b）在加热液体表面，从气泡底部受热区域流向气泡顶部较冷区域的热梯度驱动的Marangoni效应原理图，比例尺：3 mm；（c）由挥发性液体（如乙醇）在固着液滴表面的不均匀分布诱导的溶质Marangoni效应原理图，R为液滴半径，d为液滴右边界与毛细管（内含挥发性液体）左端的距离

Fig. 3 Schematic diagrams of three different driving modes of Marangoni effect: Schematic diagrams of (a) Photothermal Marangoni effect induced by temperature gradient between laser irradiation area and droplet boundary area; (b) Marangoni effect driven by thermal gradient from the heated area at the bottom of a bubble to the cold area on the top of the gas bubble; (c) Solute Marangoni effect induced by uneven distribution of volatile liquid (such as ethanol) on the surface of a sessile droplet, where R is droplet radius, and d represents the distance between the right boundary of droplet and the left end of capillary (containing volatile liquid)

3 Temperature-Driven Marangoni Effect

3.1 Photothermal Marangoni Effect of Microdroplets/Bubbles

3.1.1 Photothermal Marangoni Effect in Microdroplets

In the research on microdroplet movement based on Marangoni effects, Young et al.[5]first discovered that Marangoni forces can suspend droplets in a fluid, and the instantaneous temperature gradient causes the droplets to move towards hotter points. Their innovative discovery laid the foundation for scientists to study Marangoni effects in droplets[57⇓⇓⇓⇓⇓⇓⇓⇓~66]. Hwang et al.[33]proposed a method to drive droplets based on the photothermal Marangoni effect, which allows for precise control of droplets on various surfaces (lubricated surfaces, superamphiphobic surfaces, lubricating oil-impregnated surfaces). For single-component droplets, the control by the Marangoni flow generated from the photothermal Marangoni effect depends solely on the temperature gradient, pushing the microdroplet from the heated side to the unheated side. For multi-component droplets, depending on the type of liquid mixture, the photothermal Marangoni effect can make the droplet move at different speeds, or even in reverse directions. Figure 4shows the process of controlling polypyrrole (PPy) droplets with near-infrared (NIR) laser. PPy droplets start to move under the irradiation of near-infrared light (with a temperature difference of approximately 2.8 ℃ between the two ends of the droplet), then gradually accelerate until they reach a constant speed (Figure 4a). However, under the same experimental conditions, deionized water droplets do not move (Figure 4b), confirming that the movement of PPy droplets in Figure 4ais driven by the photothermal effect, i.e., local irradiation of near-infrared light on PPy droplets creates a temperature gradient at both ends of the droplet, generating Marangoni flow through the surface tension gradient along the droplet-air interface (Figure 4c). When the Marangoni force applied to the droplet is greater than the frictional force at the solid-liquid contact surface, the droplet will move. The photothermal Marangoni effect can easily achieve non-contact control of droplets[67⇓⇓~70], and by adjusting the power, irradiation position, and area of the laser, it enables more precise and controllable movement of the droplets[71]. Compared to control methods such as electrostatic charges, magnetic attraction, and thermocapillary convection, the manipulation of droplet movement using Marangoni effects is more convenient and efficient[72].
图4 近场红外激光对聚吡咯液滴的控制过程（a）纳米颗粒质量分数为1%，体积为10 µL的聚吡咯（PPy）液滴在润滑表面（Lubricated Surfaces）上的运动；（b）近红外辐射下去离子水液滴（10 µL）在润滑表面（LuS）上的运动；（c）近红外辐射驱动下润滑表面（LuS）上PPy液滴运动的原理图[33]

Fig. 4 Manipulation process of a polypyrrole droplet by near-infrared (NIR) laser: Motion of (a) a polypyrrole droplet and (b) a deionized water droplet on lubricated surface; (c) schematic diagram of polypyrrole droplet motion on lubricated surface driven by near-infrared radiation[33]

The photothermal Marangoni effect can also control fluid flow and particle transport within droplets. Gupta et al.[73] systematically studied the Marangoni flow and curvature-induced vortex formation in copper sulfate pentahydrate solutions using a laser-driven method. By adding dispersed carbon nanotubes (Carbon nanotubes, CNTs) into the copper sulfate pentahydrate solution for visualization, two symmetrical vortices were observed, and it was found that the CNTs accumulated around the vortices (as shown in Figure 5). Figure 5 (a~d) shows the morphology of the Marangoni vortices and the deposition of CNTs at different magnifications. As the numerical aperture of the objective lens increased, the angular velocity of the vortices increased, and so did the accumulation rate of CNTs in the vortices. This discovery is of great significance for studying the behavior of deposited particles at the microscale. Figure 5 (e, f) are simulation results of the Marangoni flow[73]. From Figure 5 (e), it can be seen that the temperature rise near the laser focus is quite significant, while the temperature rise away from the laser focus gradually becomes milder; Figure 5 (f) shows the velocity field distribution in the x-y plane and the formation of two vortices. The laser beam generates a temperature gradient in the droplet, leading to a convective force pointing towards the laser beam inside the droplet. At the same time, due to the uneven heating on the surface of the droplet, a surface tension gradient is generated, inducing a Marangoni force along the surface of the droplet away from the laser beam. When these forces overcome the dissipative forces, the fluid begins to move in a circular motion. The liquid first moves along the surface away from the laser, then flows back in large quantities towards the area illuminated by the laser.
图5 Marangoni流和曲率诱导的涡旋（a) 4×放大倍数，（b) 10×放大倍数，（c) 20×放大倍数，（d) 40×放大倍数时，碳纳米管在涡旋区的聚集情况。白色圆圈表示激光聚焦的位置（e）焦平面上激光光斑处的温度场模拟（f）焦平面上激光光斑处的速度场模拟[73]

Fig. 5 Vortex induced by Marangoni flow and curvature: The aggregation of carbon nanotubes in the vortex region (a) 4× magnification; (b) 10× magnification; (c) 20× magnification and (d) 40× magnification. The white circle indicates where the laser is focused; (e) simulation of temperature field at the laser spot on the focal plane and (f) simulation of velocity field at the laser spot on the focal plane [73]

Similarly, Goy et al.[74] utilized photothermal Marangoni flow to drive particle deposition inside droplets. The annular Marangoni flow generated by the laser concentrates particles around the laser beam, and by adjusting the parameters of the laser, the size of the Marangoni vortex region can be controlled, as well as the final deposition of the particles. Photothermal Marangoni phenomena in droplets can occur at relatively small temperature gradients and are very easy to control. The photothermal Marangoni effect is crucial for controlling droplets in biochemical analysis processes[75], and it also provides a promising control method for microfluidic technology.

3.1.2 Photothermal Marangoni Effect of Microbubbles

The use of light-captured bubbles in optofluidics research has broad application prospects[76], optical tweezers can capture dielectric particles suspended in a liquid medium through tightly focused laser beams[6,77⇓ ~79], but the trapping force is weaker when capturing larger objects such as bubbles. In recent years, the photothermal Marangoni effect has played an important role in controlling bubbles and has been widely used for steady-state manipulation of bubbles and their surrounding materials in multiphase flows[80]. The photothermal Marangoni effect heats the surface of the bubble with a laser, creating a temperature-induced tension gradient on the bubble's surface, thus triggering the Marangoni effect[81]. The photothermal Marangoni effect around the bubble can drive fluids or particles to move in a vortex-like manner[82⇓~84], thereby efficiently capturing and enriching particles. Moreover, under certain conditions, the bubble itself can also be controlled and moved by the photothermal Marangoni effect[85⇓~87].
Miniewicz et al.[88] proposed a mechanism for capturing microbubbles using the photothermal Marangoni effect: trapping bubbles within a thin layer between two glass plates filled with light-absorbing liquid, heating the liquid with a laser, and when a temperature gradient is formed on the surface of the bubble, the photothermal Marangoni effect generates vortices at the surface of the bubble. These vortices flow from the higher-temperature region to the lower-temperature regions located on both sides of the bubble, and once the pressure difference force generated by this process becomes large enough to overcome the inertial force of the bubble, the bubble starts to move. In Figure 6a, soot particles approach the surface of the bubble under the influence of the Marangoni flow and then accelerate along the gas-liquid interface. Figure 6b shows the particle trajectories obtained through COMSOL simulation, which are in good agreement with the phenomena observed in experiments. Figure 6c demonstrates the process of long-distance capture of bubbles using the photothermal Marangoni effect in experiments, where the position of the laser beam can be moved to transport the bubble to the target location.
图6 光热Marangoni效应捕获微气泡（a）含有溶解染料的液体溶液吸收激光诱导表面Marangoni流动的可视化和（b）仿真得到的粒子的轨迹与速度分布图像，红色表示速度快，蓝色表示速度慢；（c）气泡被Marangoni效应捕获的现象示例，箭头表示气泡移动方向[88]

Fig. 6 Microbubbles captured by photothermal Marangoni effect:(a) visualization of laser-induced surface Marangoni flow absorbed by a liquid solution containing dissolved dyes; (b) simulated particle trajectory and velocity distribution images, red colour indicates fast velocity and blue colour indicates slow velocity; (c) an example of a gas bubble captured by Marangoni effect, the arrows indicates the direction of bubble movement [88]

Similarly, Takeuchi et al.[46] used a laser beam to irradiate the liquid near bubbles attached to the microchannel walls, causing Marangoni convection and generating a pressure difference around the bubbles. When this pressure difference overcomes the anchoring force between the bubble and the wall, the bubble detaches from the wall; it then moves with the movement of the laser spot, thereby achieving flexible control of the bubble. It is also possible to realize bubble capture and movement by utilizing photothermal Marangoni effects generated through the absorption of light energy by metallic thin films on substrates or semiconducting nanoparticles suspended in liquids. Namura et al.[89] utilized the thermal plasmonic effect of gold nanoparticles to generate rapid Marangoni vortices around microbubbles via laser-driven methods and controlled the direction of vortex flow. This flow direction change was achieved through the thermoplastic effect of gold nanoparticles and the rapid response of the photothermal Marangoni effect at the bubble surface. In another experiment, Namura[90] studied Marangoni flows around water vapor microbubbles in degassed and non-degassed water using the thermal plasmonic effect of gold nanoisland films (GNF). A laser focused on the GNF produced stable water vapor microbubbles with a diameter of about 10 μm in degassed water (as shown in Figure 7b), and according to the visualization results of polystyrene (PS) beads (small black dots, Figure 7b), strong rotational flow appeared throughout the observation area. The liquid was attracted to the bubble surface and ejected perpendicular to the substrate surface; whereas in non-degassed water, bubbles larger than 40 μm were produced (as shown in Figure 7a), with the fluid around the bubble moving from the hot region near the laser spot to the cold region along the bubble surface, generating a rotational flow whose range was much smaller than that around the microbubbles in degassed water. The photothermal Marangoni effect-driven flow around microbubbles can not only be used for microfluidic mixing but also for sorting and manipulating particles in microchannels, showing great potential in the manipulation of particles required in biological fields.
图7 未脱气水和脱气水中的水蒸气气泡周围的Marangoni流动：（a）未脱气水中气泡和（b）脱气水中水蒸气微泡周围的流体流动。小黑点是聚苯乙烯（PS）球体，用来可视化流体运动。PS球的轨迹表示与气泡周围的旋转流相比，蒸气泡周围的旋转流更快而且更大。（c）、（d）分别给出了（a）、（b）中的流动方向的示意图[90]

Fig. 7 Marangoni Flow around a vapor bubble in degassed and undegassed water: Fluid flow around (a) air bubble in undegassed water and (b) vapor bubble in degassed water. The small black dots are polystyrene (PS) spheres that are used to visualize fluid movement. The trajectory of PS balls indicates that the rotating flow around the vapor bubble is faster and larger as compared with that around the air bubble; (c) and (d) gives a sketch of the flow directions in (a) and (b) respectively[90]

Currently, there are still many challenges in achieving three-dimensional manipulation of bubbles. Research on bubble behavior is mainly conducted by designing structured surfaces to confine the movement of bubbles within a certain plane, or by utilizing specific liquids with a certain concentration gradient, which greatly limits the practical applications based on bubble manipulation[91,92]. Hu et al.[93] used near-infrared laser irradiation on liquid to generate a spontaneously bouncing bubble. The study found that the bouncing behavior of the bubble is closely related to the existence of a temperature inversion layer (TIL). The formation of TIL generates a photothermal Marangoni flow related to the depth of the liquid, thereby causing the bubble to bounce (Figure 8a). When the bubble moves in the liquid, both buoyancy and the Marangoni force point upwards, allowing the bubble to reach the solid wall as expected. As the bubble approaches the top, the buoyancy remains constant, while the upward Marangoni force ( ) gradually decreases, and the downward Marangoni force ( 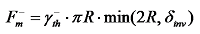) starts to increase significantly (where represents the thickness of the TIL, and 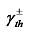represents the surface tension gradient), causing the bubble to move downwards. With changes in the position and motion state of the bubble (Figure 8b, c), the direction of the thermal Marangoni force switches from upward to downward, leading to the bouncing behavior of the bubble. The flow field simulation in Figure 8(d) shows the direction change of the Marangoni flow, inducing the reverse movement of the bubble (t=(t 0+15) ms).
图8 自发弹跳气泡(a)实验装置示意图以及在近红外激光(波长为980 nm，P= 15 W)照射水面后，水中产生的气泡弹跳过程的图像(红色框中呈现了气泡弹跳行为的两个典型周期，t=0 s表示气泡可见之前的时刻；Ht和Hc分别表示气泡的顶部和中心到水面的距离)；(b)表示气泡在液体中运动时的浮力和热Marangoni力的变化过程(c)表示靠近壁面运动时气泡受到的浮力和热Marangoni力的变化关系；(d) 弹跳气泡速度场的数值模拟图像；(e)气泡(ii和iii)与弹跳气泡(i)(移动速度为5 mm/s)的聚结过程。(f) 从侧面和顶面观察了正己烷液滴对弹跳气泡的包裹作用，形成了核壳结构的气泡-液滴复合物。(g) 激光诱导下的弹跳气泡在扫过水面时，收集到直径为80 μm的PS微珠，比例尺：200 μm[93]

Fig. 8 Spontaneous bouncing bubbles:(a)Schematic diagram of the experimental setup and images showing the bubble bouncing process generated in water after the near-infrared laser (wave length 980 nm, P= 15 W) irradiating the water (the red box presents two typical cycles of the bubble bouncing behavior, t=0 s represents the moment before the bubble is visible; Ht and Hc indicate the distance from the top and center of the bubble to the water surface, respectively). The change in buoyancy and thermal Marangoni force for (b) a bubble moving in the liquid and for (c) the bubble moving near the wall; (d) The numerical simulation results showing the velocity field of a bouncing bubble; (e) The coalescence process of bubbles; (f) Side and top views about the core shell structure of bubble droplet composite material obtained by encapsulating dancing bubbles with dye hexane droplets; (g) Particle (PS beads with diameter of 80 μm) collection onto the surface of the bouncing bubble as its sweeping through the water[93]

After elucidating the fundamental physical principles of bubbles bouncing in the vertical direction, Hu et al.[93]introduced another degree of freedom, observing the trajectory changes of the bubble as it translates with the laser beam at different horizontal velocities. Due to the temperature gradient generated by the laser during translation, the thermal Marangoni force along the xdirection pushes the bubble towards the hotter region of the laser beam. Under the action of the laser beam, the bubble exhibits good maneuverability, reaching speeds up to 40 mm/s. Furthermore, utilizing the bouncing and guiding characteristics of the bubble to control its interaction with specific objects can achieve bubble fusion (see Figure 8e), forming a core (bubble)-shell (droplet) structure (see Figure 8f), and collecting particles in liquid (see Figure 8g). This work provides research ideas for the study of three-dimensional bubble oscillation and separation based on the photothermal Marangoni effect in reality, and also offers clues for composition manufacturing based on bubbles in materials science and pollution removal in water treatment.
Similarly, Li et al[94] achieved periodic bubble bouncing by controlling the on/off of the pulsed laser during the experiment, that is, effective control over the height and frequency of bubble bouncing can be realized through simple pulsed laser control (Figure 9). This study provides new insights into flexible bubble manipulation and integration in microfluidics, advancing research in processes such as drug delivery and the development of flexible actuators.
图9 激光脉冲控制气泡弹跳高度及频率：(a)光热Marangoni效应主导的气泡向下运动的机理图，(b)在激光照射功率为57 mW时，使用COMSOL模拟的气泡开始向下移动时(ton = 2277 μs)的温度场，(c)温度和温度梯度作为在垂直方向的变化函数，(d，I)等离子体气泡向下移动过程的PIV测量图像。激光照射后，光热诱导的Marangoni流变强，推动气泡向下运动，直到气泡到达衬底，（d，II）气泡向下运动过程中温度场（图左）和流场（图右）的数值模拟，(e)在水中拍摄的等离子体泡一个周期内的光学图像，比例尺：10 μm[94]

Fig. 9 Height and frequency of a bouncing bubble controlled by laser pulse:(a) Mechanism diagram of downward movement of a gas bubble dominated by photothermal Marangoni effect; (b) Temperature field of a bubble starting to move downward simulated by COMSOL under laser irradiation with power of 57 mW; (c) temperature and temperature gradient as functions of vertical direction; (d, I) PIV measurement image showing downward movement of a plasma bubble; (d, II) Numerical simulation of temperature field (left) and flow field (right) during the downward movement of the bubble; (e) Optical image of a bouncing plasmonic bubble in water during one cycle (I, scale:10 μm) with the on/off control of laser shown in (II) [94]

3.2 Thermal Gradient Marangoni Effect of Microdroplets/Bubbles

Before the photothermal Marangoni effect was recognized, it was widely believed that if there existed a temperature gradient parallel to the free liquid surface, a thermal Marangoni force that promotes fluid flow would be generated[95]. In this case, the Marangoni effect was mostly caused by thermal gradients. In 1970, Larkin[96] first investigated the thermal gradient Marangoni effect of bubbles attached to heated surfaces, finding that the thermal Marangoni effect could slightly enhance heat transfer; O'Shaughnessy et al.[97] conducted three-dimensional simulations of the thermal gradient Marangoni effect around two bubbles on a heated wall submerged in a layer of silicone oil, and thoroughly studied their thermal interactions, discovering that as the distance between the bubbles increased, vortices could develop into larger scales, thus promoting heat transfer; Lu et al.[13] introduced groove-like surface structures in a specially designed hydrogel for solar evaporation devices, inducing the formation of thermal gradients and generating Marangoni convection, which accelerated water flow near the evaporation surface, and applied this capability to solar power generation, demonstrating the great application potential of sunlight-driven thermal gradient Marangoni flows in evaporation devices.
In addition, the Marangoni effect driven by thermal gradients also plays a very important role in the control process of bubbles/droplets[98,99], Nath et al.[36] studied the relationship between bubble lifetime and the temperature gradient between the top and bottom of the bubble, induced by the Marangoni effect due to the temperature gradient between the ambient air and the heated oil bath. The opposing effects of gravitational force on the bubble and Marangoni force maintain the bubble in a dynamic equilibrium for a certain period, prolonging its life. This phenomenon is expected to be applied in processes such as oxygen delivery in blood[100] and drug injection[101]. Although the thermally driven Marangoni effect does not require complex optical devices to provide heat energy, and the experimental setup is relatively simple, issues such as non-uniform temperature distribution and liquid layout may lead to insufficient fluid convection intensity and significant environmental impact on temperature control during operation. In contrast, photothermal driving can flexibly control the occurrence of the Marangoni effect by adjusting laser power, frequency, beam size, and position, allowing for more flexible manipulation. This is the reason why lasers are primarily used to drive the formation of the Marangoni effect in current research on controlling the behavior of bubbles/droplets.

4 Solute Marangoni Effect in Microdroplets/Bubbles

The solute Marangoni effect, caused by changes in surface tension due to concentration differences, is the reason for the formation of "wine tears" on the walls of a glass. As alcohol continuously evaporates from the surface of the wine, the alcohol concentration on the wall of the glass decreases faster, leading to a higher surface tension of the liquid on the wall compared to that in the glass. This causes the wine to move upwards along the wall, ultimately forming "wine tears"[102]. The solute Marangoni effect has been widely used in semiconductor film formation[103,104], droplet spreading[105], and bubble dynamics[34]. Over the years, researchers have conducted numerous experimental studies on controlling the movement of bubbles/droplets using the solute Marangoni effect[106⇓~108]. Baumgartner et al.[109] explored the dynamic behavior of three-component droplets composed of water, ethanol, and propylene glycol during their spreading and contraction on a glass substrate, and used such droplets to achieve the aggregation and cleaning of small-scale contaminants. Bratsun et al.[110] proposed a new design method for micro-mixers based on the combined action of the solute Marangoni effect, buoyancy convection, and diffusion. This micro-mixer is suitable for various micro-reactor systems in slightly polluted environments and holds significant importance in certain specific applications within chemical engineering[111⇓~113]. Chen et al.[114] introduced a semi-Lagrangian advection scheme, taking the methyl isobutyl ketone (MIBK)-acetic acid-water system as the research object, to study the unsteady mass transfer process of a single deformable rising droplet in the continuous phase, revealing the structure of solute Marangoni convection and simultaneously investigating the impact of Marangoni flow on the droplet mass transfer process. Park et al.[35] found that vapor-driven solute Marangoni flow can apply vapor containing volatile liquid components next to the sample, achieving control over internal droplet flow; they also used particle image velocimetry (PIV) to measure the internal flow pattern, maximum velocity, and oscillation frequency of the droplet. By changing the number of vapor sources of the volatile liquid, multiple Marangoni vortices were generated within the droplet, demonstrating that vapor-driven solute Marangoni effect is a promising mechanism for microactuators.
Figure 10shows the evolution process of the solute Marangoni effect when using ethanol (as shown in Figure 10a) and acetone (as depicted in Figures 10b-d) as vapor sources. Figure 10aillustrates the time evolution of the solute Marangoni flow, demonstrating that such a solute Marangoni vortex is induced by the diffusion of volatile solution (ethanol) vapor in the air, creating a surface tension gradient on the droplet surface, thus generating the solute Marangoni effect[115]. To test the mixing efficiency of this method, Park et al. added red dye to the pinned droplets for mixing experiments. The internal mixing processes of the droplets were tested with acetone and ethanol as vapor sources. Figures 10b-dshow the mixing evolution process of adding red dye to the pinned droplet with acetone as the vapor source; if the solute Marangoni effect is introduced, the total mixing time is significantly reduced (from 280 s to 20 s). When testing with ethanol as the vapor source, the mixing efficiency was also improved. The research by Park et al. indicates that if an appropriate volatile liquid is provided, the solute Marangoni effect induced by this liquid can serve as a feasible multi-droplet mixer or flow controller, which will help achieve low-cost and portable sample flow control in the future.
图10 溶质Marangoni流的时间演变过程：（a）乙醇蒸气源数量为1个且位于液滴右侧，橙色虚线圆圈表示液滴的接触线。（b）存在1个丙酮蒸气源时溶质Marangoni效应的混合实验；（c）存在2个丙酮蒸气源时溶质Marangoni效应的混合实验；（d）没有任何蒸气源时液滴内部的纯扩散[35]

Fig. 10 Temporal evolution of the solutal Marangoni flow:(a) The number of ethanol vapor sources is 1 and is located on the right side of the droplet, the orange-dashed circle represents the contact line of the droplet. Mixing experiments with solutal Marangoni effects; (b) one point of acetone vapor source; (c) two points of acetone vapor sources; (d) pure diffusion inside the droplet in the absence of any vapor source [35]

Under normal circumstances, diffusion within droplets, limited by evaporation, exhibits very low internal flow rates. Hegde et al.[116] proposed a non-invasive method to enhance the internal flow of droplets without affecting their overall evaporation behavior, based on the solute Marangoni effect. By asymmetrically placing an ethanol droplet near a water droplet, the high volatility of ethanol causes ethanol molecules to be adsorbed asymmetrically at the air-water interface, generating a surface tension gradient and thus inducing solute Marangoni convection inside the water droplet[117]; the flow rate is about thousands of times higher than that of naturally evaporating droplets. The intensity of the solute Marangoni convection can be altered by controlling the distance between the ethanol droplet and the water droplet, allowing for precise control over the flow within the water droplet. Droplet mixing control based on the solute Marangoni effect holds significant importance for research in the fields of lab-on-a-chip, medical diagnostics, and DNA profiling[118].
Park et al.[34] studied the bubble dynamics of hydrogen evolution reaction on platinum microelectrodes by altering the composition of the electrolyte. It was found that the solute Marangoni effect plays a crucial role in the periodic detachment process of individual H2 bubbles in sulfuric acid. Figure 11 is a schematic diagram illustrating the impact of thermal Marangoni effect and solute Marangoni effect on the evolution of H2 bubbles. The orange gradient area on the left side of the figure represents the temperature field during the hydrogen evolution reaction (HER) process, with the thermal Marangoni flow caused by the temperature gradient moving away from the platinum surface region (black arrows). The green gradient on the right side shows the ion concentration field during the HER process. When the increment of surface tension is negative (σc<0), the solute Marangoni flow induced by the concentration gradient moves towards the platinum surface region (red arrows); when the increment of surface tension is positive (σc>0), the solute Marangoni convection flows away from the platinum surface region[34]. In H2SO4 solution, the decrease in ion concentration near the platinum surface leads to a reduction in the local surface tension of the solution. As a result, the solute Marangoni force acts on the electrode, generating a solute Marangoni convection that moves away from the platinum surface, accelerating the separation of bubbles at the electrode surface. Since the increment of surface tension varies among different electrolytes, the solute Marangoni force acting on individual H2 bubbles also changes, meaning that the detachment behavior of bubbles during hydrogen evolution can be controlled by changing the electrolyte. This discovery allows for a deeper understanding of the dynamics of H2 bubbles at the electrode/electrolyte/bubble interface and provides valuable insights into bubble separation operations based on the solute Marangoni effect.
图11 热Marangoni效应和溶质Marangoni效应对H2气泡演化的影响[34]

Fig. 11 Influence of thermal Marangoni effect and solute Marangoni effect on H2 bubble evolution[34]

5 Applications of the Marangoni Effect in Microdroplets/Bubbles

The Marangoni effect plays a significant role in applications based on microbubble/droplet manipulation, with its unique generation mechanism being irreplaceable in the movement, separation, and bouncing control of microbubbles/droplets[52,119]. Research by Basu et al.[31] has shown that Marangoni flow in microfluidics can be designed by altering the geometry of the heat source (point, linear, or annular), and such Marangoni flows can be used to simulate a wide range of microdroplet operations, including mixing, confinement, filtration, and capture. This programmable system is particularly important for research applications requiring high flexibility. Karpitschka et al.[106] studied, both theoretically and experimentally, the Marangoni contraction phenomenon of sessile droplets of volatile and non-volatile binary mixtures, providing a power-law relationship between the quasi-static contact angle and the relative saturation of the vapor phase. This Marangoni contraction phenomenon is anticipated to be utilized for cleaning/drying semiconductor surfaces and for multi-scale solute patterning deposition. Takeuchi et al.[46] used optical techniques to control the Marangoni forces around bubbles, enabling the movement or detachment of bubbles from walls, which can be applied to remove bubbles adhering to channel walls, addressing issues such as pressure loss and equipment degradation. Manjare et al.[120] confirmed through simulations that the direction and intensity of the Marangoni flow are consistent with the observed motion of spherical Janus catalytic micromotors, suggesting that the Marangoni effect occurring around these micromotors can be applied to cargo transport, selective detection, and targeted nucleic acid delivery at micro- and nanoscales; furthermore, the Marangoni effect can also be applied to the dissolution process of droplets in multiphase flows. Encarnación et al.[121] investigated four distinctly different dissolution stages of alcohol droplets in water, where the presence of the Marangoni effect significantly enhanced each dissolution stage. Similar studies on droplet dissolution processes have been widely applied in diagnostics, food industry, and inkjet printing.
The Marangoni effect has also demonstrated its advantages of non-contact, high controllability, and high conversion efficiency in the preparation and driving of various novel structures and devices. It is particularly important for research in areas such as surface microstructure preparation, bubble-pen lithography, multiphase droplet actuation, droplet motor braking, and emulsion energy supply.

5.1 Preparation of Surface Microstructures

Optothermally induced bubbles have been widely used for the preparation of various surface microstructures. Wang et al.[21] achieved the deposition of PS particles in solution at the three-phase contact line of the bubble through the Marangoni effect around the plasma bubble, producing 3D surface microstructures (Figure 12). By adjusting parameters such as the cycle time of the plasma bubble, the concentration of PS particles, and the diameter of the laser spot, the height and width of the microstructure can be well regulated, demonstrating good controllability throughout the entire manufacturing process. This method facilitates our exploration of the applications of surface microstructures in microelectromechanical systems[122], supercapacitors[123], and optoelectronics[124], providing a way to utilize optothermal microbubbles for the fabrication of three-dimensional microstructures.
图12 3D表面微结构制造：（a）由于等离子体效应，气泡周围的热Marangoni流将PS微粒运输到三相接触线。（b）关闭激光后，气泡从基板上分离并上升，在基板上留下微结构。(c)等离子体气泡的反复成核并分离导致PS微粒在底部积累，(d)等离子体气泡重复成核，最终形成了三维微柱，(e)表面微结构产生后等离子体气泡周围的Marangoni对流仿真图像，(f)(f，Ⅰ)在激光功率为302 mW，在占空比为ton(单个周期中激光打开的时间)=200 ms，toff(单个周期中激光关闭的时间)=200 ms，N(气泡重复成核的次数)=100，c(PS浓度)=150 μg/mL时，5倍物镜观测下三维微结构的等距扫描电子显微镜图像。（f，II)、(f，III）和（f，IV）分别是（f，Ⅰ）中所示的1、2、3三个选定区域的扫描电子显微镜图像，（g）在没有表面微结构和有表面微结构（h）的情况下通过跟踪流体中PS微粒的运动构建的Marangoni对流流线[21]

Fig. 12 3D fabrication of surface microstructure:(a) The transport of PS particles to the three-phase contact line due to the plasma effect in the presence of a hot Marangoni flow around a bubble; (b) The bubble detaches from the substrate once the laser is turned off, leaving behind a microstructure on the substrate; (c) The repeated nucleation and separation of plasma bubbles result in the accumulation of PS particles at the bottom; (d) The repeated nucleation of plasma bubbles eventually leads to the formation of a three-dimensional microcolumn; (e) The image shows a simulation of Marangoni convection around a plasma bubble after the generation of surface microstructure; (f, I) An isometric view of SEM image showing an obtained microstructure with a 5× objective lens, the experimental parameters used were Pl = 302 mW, ton = 200 ms, toff = 200 ms, N = 100, and c = 150 μg/mL， (f, II), (f, III), and (f, IV) are enlarged SEM images of three selected areas shown in (f, I); (g) The Marangoni convection streamline constructed by tracking the motion of PS particles in the fluid without surface microstructure; (h) Conversely, with the surface microstructure present, the Marangoni convection streamline is affected [21]

5.2 Bubble Pen Lithography

Given the current limitations of lithography technology in the patterning of chemically synthesized colloidal particles, Lin et al.[125] developed a new technique based on the photothermal Marangoni effect, known as bubble-pen lithography (BPL). This technique utilizes the photothermal Marangoni effect to generate microbubbles at the interface between the colloidal suspension and the plasmonic substrate. The microbubbles, through the synergistic action of Marangoni convection, surface tension, gas pressure, and substrate adhesion, capture and fix colloidal particles onto the substrate. By guiding the laser beam to move the microbubbles, BPL is capable of writing arbitrary patterns of single particles and particle clusters in two-dimensional or three-dimensional configurations. Figure 13 illustrates the principle of capturing colloidal particles by microbubbles based on the Marangoni effect on a gold substrate surface, as well as the patterns formed by PS microspheres of different sizes on the plasmonic substrate.
图13 等离子体增强光热效应气泡笔光刻：（a）单个微泡捕获粒子机制的示意图（截面图）。蓝色球体表示去离子水中的悬浮粒子。由于摩擦力的作用，粒子沿着Marangoni对流流动。插图显示了粒子被微气泡捕获时的力分布（红色虚线表示）。PB和PL分别表示气泡中的压力和液体中的压力，它们产生将粒子向外推的净力FP。表面张力FS产生拖曳力FD。（b）在AuNIs基板上连续写入540 nm PS小球直线图案的时间分辨过程，比例尺：50 μm。（c) 540 nmPS小球的“SP”图案的暗场光学图像，比例尺：10 μm。（d) 60 nm PS小球的4×4阵列三维空心结构的暗场光学图像，比例尺：10 μm[125]

Fig. 13 Plasma-enhanced photothermal bubble pen lithography:(a) Schematic diagram of the particle trapping mechanism of a single microbubble. The blue spheres represent suspended particles in deionized water. These particles flow convection along the Marangoni due to friction. As shown in the inset, a particle is captured by the microbubble indicated by the dotted red line. The inner pressure of the bubble (PB) and the pressure in the liquid (PL) produce a net force (FP) that pushes the particles outward. Additionally, the surface tension (FS) introduces a drag force (FD), as illustrated; (b) Time-resolved process of continuous writing in straight line pattern performed on the AuNIs substrate (with 540 nm PS bead, scale: 50 μm); (c) Dark field optical image revealing the formation of the "SP" letter pattern (540 nm PS beads, scale :10 μm); (d) Dark field optical image demonstrating a 4×4 array of 3D hollow structures (60 nm PS beads, scale:10 μm) [125]

5.3 Multiphase Droplet Actuation

The control of multi-component droplets is also one of the important applications of the Marangoni effect[120,126⇓⇓⇓ ~130]. Nagelberg et al.[20] proposed a novel droplet driving mechanism, utilizing an optically induced thermal gradient to generate an interfacial tension difference at the capillary interface inside Janus droplets (fluorinated surfactant), thereby causing Marangoni flow and net torque within the droplet, allowing for predictable and controllable reorientation of the droplet, as shown in Figure 14. Biphasic droplets formed by immiscible hydrocarbons and fluorocarbons produce small temperature gradients in the fluid medium through focused near-infrared lasers (Figure 14a), which induce interfacial tension gradients that generate Marangoni flow and net torque on the side of the droplet, leading to reorientation of the droplet (Figure 14b-e). This method of using optical means to induce the Marangoni effect for multiphase droplet rotation is of great significance in fields such as microfluidic sorting, droplet mixing, and microreactors, and it is also a promising control mechanism for droplet-based micro-optical components[131].
图14 乳化液滴朝向激光点重新定位：（a）庚烷和全氟己烷形成的乳化液滴旋转朝向热源重新定位过程，比例尺为50 µm。（b）仅受重力影响时，由较轻碳氢化合物（粉红色）和较重氟碳化合物（灰色）形成的乳化液滴的俯视图；（c）热源经过时乳化液滴的俯视图示意图；（d）同一液滴的侧视图示意图，γH、γF和γFH分别为碳氢化合物、氟碳化合物、两种化合物接触面的界面张力；（e) 液滴内部毛细表面形成界面张力梯度，使液滴在平衡热Marangoni力扭矩τth和重力扭矩τg的情况下呈稳态倾斜。Rd：液滴半径，Rcm：重心到质心的距离，Fg：重力[20]

Fig. 14 Repositioning of emulsion droplets toward the laser point:(a) Emulsion droplets consisting of perfluorohexane and heptane were observed to rotate towards the heat source (scale: 50 µm); (b) and (c) present top-views of the emulsion droplets formed from lighter hydrocarbons (pink) and heavier fluorocarbons (grey), (b) under the influence of gravity alone and (c) when a heat source passed by; (d) presents a side view of the same droplet, where γH, γF and γHF are the relevant interfacial tension; (e) An interfacial tension gradient forms at the internal capillary surface of the droplet in a thermal field, and this gradient results in a steady-state tilt with the condition that the thermal Marangoni force torque τth and the gravitational torque τg are balanced. Here, Rd represents the droplet radius, Rcm denotes the distance from the center of gravity to the center of mass, and Fg represents gravity[20]

5.4 Droplet Motor

Zhang et al.[132]investigated the solute Marangoni effect of polyvinylidene fluoride/dimethyl formamide (PVDF/DMF) concentrated droplets, achieving rapid rotation of PVDF/DMF droplets. As shown in Figure 15, when a PVDF/DMF droplet (concentration 45 mg/mL) is placed on a horizontal surface, due to the different surface tensions of the two liquid phases, a solute Marangoni effect occurs, where DMF on the surface preferentially and rapidly diffuses into water, generating a high thrust force that prompts the droplet to rotate quickly. This energy transfer process based on the Marangoni effect is similar to biological motors based on dissipative chemical energy, which can be conveniently integrated with other devices or actuators. Compared to existing mechanical motion systems, it has significant advantages such as no noise, no air pollution, and no unnecessary exhaust emissions.
图15 高速转动的浓缩液滴将动能转化为电能和机械能的示意图[132]

Fig. 15 Schematic image illustrating the conversion process of kinetic energy into electrical and mechanical energy by a concentrated droplet[132]

5.5 Emulsified Energy Supply

Oil/water emulsions can significantly alter the fluidity of oil, thereby greatly improving recovery rates. Zhang et al.[133] observed Marangoni effect-induced turbulence at the oil/water interface under low shear stress (Figure 16a,b). Due to the differences in the absorption rate of nanoemulsion particles at the oil/water interface, local interfacial tension varies; fluids move from areas of low interfacial tension to high interfacial tension, generating a Marangoni effect and causing turbulence (Figure 16c). Nanoemulsions, water, and organic solutions penetrate into the oil through mass transfer and dissolution, thus promoting the formation of emulsions (Figure 16d). The Marangoni effect occurring at the interface between oil droplets and water can convert interfacial energy into kinetic energy, change the shape of oil droplets, promote the formation of oil/water emulsions, reduce the adsorption of heavy oil on oil sands, provide kinetic energy for emulsification, and improve the recovery rate of heavy oil by water flooding.
图16 油/水界面Marangoni效应诱发湍流：（a）Marangoni效应（湍流）产生前油水界面的状况；（b）Marangoni效应（湍流）产生时油水界面的状况；（c）Marangoni效应引发湍流的示意图；（d）Marangoni效应的传质[133]

Fig. 16 Turbulence induced by Marangoni effect at the oil/water interface:(a) The oil-water interface at the beginning of the Marangoni effect (turbulence); (b) The oil-water interface in the process of the Marangoni effect (turbulence); (c) Schematic diagram of turbulenc caused by Marangoni effect; (d) Mass transfer of the Marangoni effect [133]

In summary, the Marangoni effect based on microdroplets/bubbles provides an efficient driving method for research in fields such as materials science, biological sciences, and chemical industries. The uniqueness of the Marangoni effect lies in its ability to induce convection within fluids, causing bubbles and droplets to move between regions of different temperatures or concentrations, thus it is widely applied in the manipulation of microdroplets/bubbles. In microfluidic systems, the Marangoni effect can more precisely control the movement, aggregation, and separation of tiny droplets, offering advantages for designs such as microreactors or microfluidic chips. Compared to other driving methods, the Marangoni effect can be generated without external devices and auxiliary controls, simplifying the system and reducing complexity. Additionally, during the process of manipulating microdroplets/bubbles, the Marangoni effect exhibits excellent temperature controllability, rapid response, and ease of control, making it broadly applicable across disciplines including biology, chemistry, and medicine. However, it should be noted that accomplishing these tasks typically requires relatively complex laser setups, and utilizing light-induced Marangoni effects necessitates localized heating or adding photosensitive surfactants to the liquid, which can lead to sample contamination; this is particularly disadvantageous for bubble/droplet-related applications in biomedicine, greatly limiting its application. Therefore, how to achieve precise control over droplets/bubbles in non-ideal real-world environments without affecting the final outcome of experiments is a direction we need to strive towards in the future.

6 Conclusions and Prospects

The Marangoni effect in heat and mass transfer processes has demonstrated unique advantages in the manipulation of microdroplets/bubbles, allowing us to induce the formation of surface tension gradients through lasers, temperature gradients, or concentration gradients, thereby achieving the movement, coalescence, and separation control of microdroplets/bubbles[134,135], and providing some new methods for research in fields such as biology, chemistry, and medicine[136]. This article elaborates on the causes and control methods of photothermal Marangoni effects, thermal gradient Marangoni effects, and solute Marangoni effects during bubble/droplet manipulation through several typical cases. In addition, it categorizes and summarizes recent advanced applications based on Marangoni effect-driven microbubble/droplet manipulation, introducing their ingenious use in the preparation of surface microstructures, optically controlled technologies, multiphase droplet actuation, droplet motor braking, and emulsion energy supply processes. Finally, it discusses the shortcomings of the Marangoni effect in controlling microbubbles/droplets and future breakthrough directions. In summary, we hope that the latest progress in manipulating microbubbles/droplets using the Marangoni effect can stimulate interest in the study of Marangoni phenomena and achieve rapid breakthroughs of the Marangoni effect in various fields.

References

Publishing order | Descend order by publishing year | Descend order by cited within
[1]
Thomson J. Lond. Edinb. Dublin Philos. Mag. J. Sci., 1855, 10(67): 330.

[2]
Marangoni C. Sull'espansione delle goccie d'un liquido galleggianti sulla superfice di altro liquido (Fratelli Fusi). 1865.

[3]
Hu X W, Sun M, Zheng J G, Jiang H Q. IOP Conf. Ser. Earth Environ. Sci., 2021, 675(1): 012187.

[4]
Nabavizadeh S A, Eshraghi M, Felicelli S D, Tewari S N, Grugel R N. Int. J. Multiphase Flow, 2019, 116: 137.

[5]
Young N O, Goldstein J S, Block M J. J. Fluid Mech., 1959, 6(3): 350.

[6]
Ashkin A, Dziedzic J M, Bjorkholm J E, Chu S. Opt. Lett., 1986, 11(5): 288.

[7]
Cazabat A M, Heslot F, Troian S M, Carles P. Nature, 1990, 346(6287): 824.

[8]
Villers D, Platten J K. J. Fluid Mech., 1992, 234: 487.

[9]
Antanovskii L K. Phys. Fluids, 1995, 7(4): 747.

[10]
Saiz E, Tomsia A P. Nat. Mater., 2004, 3(12): 903.

[11]
Sempels W, De Dier R, Mizuno H, Hofkens J, Vermant J. Nat. Commun., 2013, 4: 1757.

[12]
Kim H, Muller K, Shardt O, Afkhami S, Stone H A. Nat. Phys., 2017, 13(11): 1105.

[13]
Lu Y, Fan D Q, Wang Y D, Xu H L, Lu C H, Yang X F. ACS Nano, 2021, 15(6): 10366.

[14]
Wu H, Chen Y, Xu W, Xin C, Wu T, Feng W, Yu H, Chen C, Jiang S, Zhang Y. Nat. Commun., 2023, 14(1): 20.

[15]
Linde H, Velarde M G, Waldhelm W, Loeschcke K, Wierschem A. Ind. Eng. Chem. Res., 2005, 44(5): 1396.

[16]
Zhang Y, Zheng L C, Zhang X X. Acta Phys. Sin., 2009, 58(8): 5501.

(张艳, 郑连存, 张欣欣. 物理学报, 2009, 58(08): 5501.)

[17]
Hershey A V. Phys. Rev., 1939, 56(2): 204.

[18]
Berg S. Phys. Fluids, 2009, 21(3): 032105.

[19]
Chen S Y, Yuan X G, Fu B, Yu K. Front. Chem. Sci. Eng., 2011, 5(4): 448.

[20]
Nagelberg S, Totz J F, Mittasch M, Sresht V, Zeininger L, Swager T M, Kreysing M, Kolle M. Phys. Rev. Lett., 2021, 127(14): 144503.

[21]
Wang F L, Dong L H, Wang Z Y, Chen B Y, Zhu Y J, Tong Z, Wang H M, Wang Y L. Surf. Interfaces, 2024, 44: 103710.

[22]
Chen J, Shen C Q, Wang H, Zhang C B. Acta Phys. Sin., 2019, 68(7): 183.

(陈俊, 沈超群, 王贺, 张程宾. 物理学报, 2019, 68(7): 183.)

[23]
OShaughnessy S M, Robinson A J. Microgravity Sci. Technol., 2008, 20(3): 319.

[24]
OShaughnessy S M, Robinson A J. Heat Transf. Eng., 2009, 30(13): 1096.

[25]
OShaughnessy S M, Robinson A J. Ann. N Y Acad. Sci., 2009, 1161(1): 304.

[26]
Bezuglyi B A, Ivanova N A. Tech. Phys. Lett., 2002, 28(10): 828.

[27]
Ivanova N A, Bezuglyi B A. J. Appl. Mech. Tech. Phys., 2005, 46(5): 691.

[28]
Buffone C, Sefiane K, Christy J R E. Phys. Fluids, 2005, 17(5): 052104.

[29]
Wang H, Peng X F, Christopher D M, Lin W K, Pan C. Int. J. Heat Fluid Flow, 2005, 26(3): 485.

[30]
Baroud C N, Robert de Saint Vincent M, Delville J P. Lab a Chip, 2007, 7(8): 1029.

[31]
Basu A S, Gianchandani Y B. J. Micromech. Microeng., 2008, 18(11): 115031.

[32]
Delville J P, Robert de Saint Vincent M, Schroll R D, Chraïbi H, Issenmann B, Wunenburger R, Lasseux D, Zhang W W, Brasselet E. J. Opt. A: Pure Appl. Opt., 2009, 11(3): 034015.

[33]
Hwang H, Papadopoulos P, Fujii S, Wooh S. Adv. Funct. Mater., 2022, 32(15): 2111311.

[34]
Park S, Liu L H, Demirkır C, van der Heijden O, Lohse D, Krug D, Koper M T M. Nat. Chem., 2023, 15(11): 1532.

[35]
Park J, Ryu J, Sung H J, Kim H. J. Colloid Interface Sci., 2020, 561: 408.

[36]
Nath S, Ricard G, Jin P L, Bouillant A, Quere D. Soft Matter, 2022, 18(38): 7422.

[37]
Karbalaei A, Kumar R, Cho H. Micromachines, 2016, 7(1): 13.

[38]
Namura K, Nakajima K, Kimura K, Suzuki M. Appl. Phys. Lett., 2016, 108(7): 071603.

[39]
Muñoz-Pérez F M, Ortega-Mendoza J G, Padilla-Vivanco A, Toxqui-Quitl C, Sarabia-Alonso J A, Ramos-García R. Front. Phys., 2020, 8: 585590.

[40]
Morris C J, Parviz B A. J. Micromech. Microeng., 2006, 16(5): 972.

[41]
Hu X Z, Chen Y P, Ni B Q, Yu X J. Acta Phys-chim. Sin., 1998, 14(2): 136.

(胡学铮, 陈烨璞, 倪邦庆, 虞学俊. 物理化学学报, 1998, 14(2): 136.)

[42]
Cira N J, Benusiglio A, Prakash M. Nature, 2015, 519(7544): 446.

[43]
Lu H H, Yang Y M, Maa J R. Ind. Eng. Chem. Res., 1997, 36(2): 474.

[44]
Lu H H, Yang Y M, Maa J R. Ind. Eng. Chem. Res., 1996, 35(6): 1921.

[45]
Takahashi K, Weng J G, Tien C L. Microscale Thermophys. Eng., 1999, 3(3): 169.

[46]
Takeuchi H, Motosuke M, Honami S. Heat Transfer Eng., 2012, 33(3): 234.

[47]
Farahi R H, Passian A, Zahrai S, Lereu A L, Ferrell T L, Thundat T. Ultramicroscopy, 2006, 1068-9: 815.

[48]
Farahi R H, Passian A, Ferrell T L, Thundat T. Appl. Phys. Lett., 2004, 85(18): 4237.

[49]
Basu A S, Gianchandani Y B. Appl. Phys. Lett., 2007, 90(3): 034102.

[50]
Butzhammer L, Köhler W. Microfluid. Nanofluid., 2017, 21(10): 155.

[51]
Sha Y, Cheng H, Yu G C. Prog. Chem., 2003, 15(01): 9.

(沙勇, 成弘, 余国琮. 化学进展, 2003, 15(01): 9.)

[52]
Tang X X, Chen H Y, Wang J J, Wang Z J, Zang D Y. Acta Phys. Sin., 2023, 72(19): 194.

(唐修行, 陈泓樾, 王婧婧, 王志军, 臧渡洋. 物理学报, 2023, 72(19): 194.)

[53]
Qin W G, Wang J, Ji W J, Zhao W J, Chen C, Lan D, Wang Y R. Acta Phys. Sin., 2022, 71(06): 359.

(秦威广, 王进, 纪文杰, 赵文景, 陈聪, 蓝鼎, 王育人. 物理学报, 2022, 71(06): 359.)

[54]
Hu X Z. Acta Phys-chim. Sin., 1997, 13(10): 873.

(胡学铮. 物理化学学报, 1997, 13(10): 873.)

[55]
Wu K. Acta Phys-chim. Sin., 2019, 35(11): 1183.

(吴凯. 物理化学学报, 2019, 35(11): 1183.)

[56]
Hu H, Larson R G. Langmuir, 2005, 21(9): 3972.

[57]
Savino R, Paterna D, Favaloro N. J. Thermophys. Heat Transf., 2002, 16(4): 562.

[58]
Girard F, Antoni M, Faure S, Steinchen A. Langmuir, 2006, 22(26): 11085.

[59]
Kazemi M A, Saber S, Elliott J A W, Nobes D S. Int. J. Heat Mass Transf., 2021, 181: 122042.

[60]
Schmitt M, Stark H. Phys. Fluids, 2016, 28(1):012106.

[61]
Saeedian Tareie Z, Latifi H, Parchegani S, Soltanlou K. Opt. Laser Technol., 2019, 120: 105749.

[62]
Yang Q J, Mao Q, Cao W. Colloids Surf. A Physicochem. Eng. Aspects, 2022, 639: 128385.

[63]
Liu H H, Zhang Y H. J. Comput. Phys., 2015, 280: 37.

[64]
Chandramohan A, Dash S, Weibel J A, Chen X M, Garimella S V. Langmuir, 2016, 32(19): 4729.

[65]
Li Z D, Zhao J F, Qin W T. J. Eng. Thermophys-Rus., 2010, 31(6): 979.

(李震东, 赵建福, 秦文韬. 工程热物理学报, 2010, 31(6): 979.)

[66]
Kawaji M, Gamache O, Hwang D H, Ichikawa N, Viola J P, Sygusch J. J. Cryst. Growth. 2003, 2583-4: 420.

[67]
Hendarto E, Gianchandani Y B. J. Micromech. Microeng., 2011, 21(11): 115028.

[68]
Li H N, Yang Y J, Zhu X, Ye D D, Yang Y, Wang H, Chen R, Liao Q. Soft Matter, 2023, 19(38): 7323.

[69]
Basu A S, Yee S Y, Gianchandani Y B. 2007 IEEE 20th International Conference on Micro Electro Mechanical Systems (MEMS). Hyogo, Japan. IEEE, 2007: 401.

[70]
Motosuke M, Hoshi A, Honami S. ICNMM., 2012, 73304: 97.

[71]
Tarafdar S, Tarasevich Y Y, Dutta Choudhury M, Dutta T, Zang D Y. Adv. Condens. Matter Phys., 2018, 2018: 5214924.

[72]
Deng H H, Zhang M, Liu H. Sci. China Chem., 2023, 53(7): 1172.

(邓环环, 张敏, 刘欢. 中国科学: 化学, 2023, 53(7): 1172.)

[73]
Gupta K, Kolwankar K M, Gore B, Dharmadhikari J A, Dharmadhikari A K. Phys. Fluids, 2020, 32(12): 121701.

[74]
Goy N A, Bruni N, Girot A, Delville J P, Delabre U. Soft Matter, 2022, 18(41): 7949.

[75]
Saeedian Tareie Z, Latifi H, Soltanlou K, Heidariazar A, Mahdi Majidof M, Lafouti M. Results Opt., 2023, 10: 100347.

[76]
Arita Y, Richards J M, Mazilu M, Spalding G C, Skelton Spesyvtseva S E, Craig D, Dholakia K. ACS Nano, 2016, 10(12): 11505.

[77]
Ashkin A. PNAS., 1997, 94(10): 4853.

[78]
Ashkin A, Dziedzic J M. Phys. Rev. Lett., 1977, 38(23): 1351.

[79]
Huo C A, Qiu S J, Liang Q M, Geng B J, Lei Z C, Wang G, Zou Y L, Tian Z Q, Yang Y. Acta Phys. Chim. Sin., 2023: 2303037.

[80]
Barthes M, Reynard C, Santini R, Tadrist L. Europhys. Lett., 2007, 77(1): 14001.

[81]
Namura K, Nakajima K, Suzuki M. Nanotechnology, 2018, 29(6): 065201.

[82]
Namura K, Nakajima K, Kimura K, Suzuki M. Appl. Phys. Lett., 2015, 106(4): 043101.

[83]
Xu C L, Shi Y C, Jin X X, Lei Z S, Zhong Y B, Guo J H. Appl. Mech. Mater., 2014, 624: 262.

[84]
Darwish A, Abdelgawad M. 2019 IEEE 14th International Conference on Nano/Micro Engineered and Molecular Systems (NEMS). Bangkok, Thailand. IEEE, 2019. 524.

[85]
Inbaoli A, Sujith Kumar C S, Jayaraj S. Appl. Therm. Eng., 2022, 214: 118805.

[86]
Sarabia-Alonso J A, Ortega-Mendoza J G, Ramírez-San-Juan J C, Zaca-Morán P, Ramírez-Ramírez J, Padilla-Vivanco A, Muñoz-Pérez F M, Ramos-García R. Opt. Express, 2020, 28(12): 17672.

[87]
Sarabia-Alonso J A, Ortega-Mendoza J G, Ascencio-Rodríguez J A, Ramos-García R, Dholakia K, Spalding G C. Proc. of SPIE., 2022, 12198:117.

[88]
Miniewicz A, Quintard C, Orlikowska H, Bartkiewicz S. Phys. Chem. Chem. Phys., 2017, 19(28): 18695.

[89]
Namura K, Nakajima K, Kimura K, Suzuki M. J. Nanophoton., 2016, 10(3): 1.

[90]
Namura K, Nakajima K, Suzuki M. Sci. Rep., 2017, 7: 45776.

[91]
Zhan H Y, Yuan Z C, Li Y, Zhang L, Liang H, Zhao Y H, Wang Z G, Zhao L, Feng S L, Liu Y H. Nat. Commun., 2023, 14: 6158.

[92]
Miniewicz A, Bartkiewicz S, Orlikowska H, Dradrach K. Sci. Rep., 2016, 6: 34787.

[93]
Hu M, Wang F, Chen L, Huo P, Li Y Q, Gu X, Chong K L, Deng D S. Nat. Commun., 2022, 13: 5749.

[94]
Li X L, Wang F L, Xia C L, Le The H, Bomer J G, Wang Y L. Small, 2023, 19(49): e2302939.

[95]
Schwabe D, Scharmann A. Adv. Space Res., 1988, 8(12): 175.

[96]
Larkin B K. AlChE. J., 1970, 16(1): 101.

[97]
O'Shaughnessy S M, Robinson A J. Int. J. Therm. Sci., 2014, 78: 101.

[98]
Bratukhin Y K, Kostarev K G, Viviani A, Zuev A L. Exp. Fluids, 2005, 38(5): 594.

[99]
Lin S X, Zhu B J, Yi Y W, Zhang Y, Liu P Y, Ma M. Chin. J. Comput. Mech., 2019, 36(1): 52.

(林圣享, 朱宝杰, 易义武, 张莹, 刘佩尧, 马明. 计算力学学报, 2019, 36(1): 52.)

[100]
Gerber F, Waton G, Krafft M P, Vandamme T F. Artif. Cells Blood Substit. Biotechnol., 2007, 35(1): 119.

[101]
Jang H J, Park M A, Sirotkin F V, Yoh J J. Appl. Phys. B, 2013, 113(3): 417.

[102]
Fournier J B, Cazabat A M. Europhys. Lett., 1992, 20(6): 517.

[103]
Wang Z A, Guo H, Rong X, Dong G F. Acta Phys-Chim. Sin., 2019, 35(11): 1259.

(王子昂, 郭航, 荣欣, 董桂芳. 物理化学学报, 2019, 35(11): 1259.)

[104]
Han G B, Wu J T, Xu X M. Acta Phys. Chim. Sin., 2000, 16(6): 507.

(韩国彬, 吴金添, 徐晓明. 物理化学学报, 2000, 16(6): 507.)

[105]
Carles P, Cazabat A M. Colloids Surf., 1989, 41: 97.

[106]
Karpitschka S, Liebig F, Riegler H. Langmuir, 2017, 33(19): 4682.

[107]
Christy J R E, Hamamoto Y, Sefiane K. Phys. Rev. Lett., 2011, 106(20): 205701.

[108]
Yiantsios S G, Serpetsi S K, Doumenc F, Guerrier B. Int. J. Heat Mass Transf., 2015, 89: 1083.

[109]
Baumgartner D A, Shiri S, Sinha S, Karpitschka S, Cira N J. Proc. Natl. Acad. Sci. U. S. A., 2022, 119(19): e2120432119.

[110]
Bratsun D, Kostarev K, Mizev A, Aland S, Mokbel M, Schwarzenberger K, Eckert K. Micromachines, 2018, 9(11): 600.

[111]
Huang Y R, Huang R W, Ma X, Li Z Z, Teng H H. Acta Mech. Sinica-Prc., 2023, 1.

(黄彦如, 黄睿雯, 马雪, 李真珍, 滕宏辉. 力学学报, 2023, 1.)

[112]
Han G B. Acta Phys-Chim. Sin., 1998, 14(8): 709.

(韩国彬. 物理化学学报, 1998, 14(8): 709.)

[113]
Wang Z A, Guo H, Li J W, Wang L D, Dong G F. Adv. Mater. Interfaces, 2019, 6(8): 1801736.

[114]
Chen J, Wang Z H, Yang C, Mao Z S. Chem. Eng. Technol., 2015, 38(1): 155.

[115]
Zhang X Q, Chen H Y, Wang Z J, Wang N, Zang D Y. Materials, 2023, 16(14): 5168.

[116]
Hegde O, Chakraborty S, Kabi P, Basu S. Phys. Fluids, 2018, 30(12): 122103.

[117]
Wang Z Z, Chen J, Feng X, Mao Z S, Yang C. Chem. Eng. Sci., 2021, 233: 116401.

[118]
Zang D Y, Tarafdar S, Tarasevich Y Y, Dutta Choudhury M, Dutta T. Phys. Rep., 2019, 804: 1.

[119]
Zeng B L, Wang Y L, Diddens C, Zandvliet H J W, Lohse D. Phys. Rev. Fluids, 2022, 7(6): 064006.

[120]
Manjare M, Yang F C, Qiao R, Zhao Y P. J. Phys. Chem. C, 2015, 119(51): 28361.

[121]
Encarnación Escobar J M, Nieland J, van Houselt A, Zhang X H, Lohse D. Soft Matter, 2020, 16(18): 4520.

[122]
Shi J, Monticone F, Elias S, Wu Y, Ratchford D, Li X, Alu A. Nat. Commun., 2014, 5(1): 3896.

[123]
Ji P Y, Zhang X, Wan J, Zhang C S, Yang Q X, Zhang X M, Gan L Y, Xi Y. Surf. Interfaces, 2022, 33: 102290.

[124]
Shu Y, Porter B F, Soh E J H, Farmakidis N, Lim S, Lu Y, Warner J H, Bhaskaran H. Nano Lett., 2021, 21(9): 3827.

[125]
Lin L, Peng X, Mao Z, Li W, Yogeesh M N, Rajeeva B B, Perillo E P, Dunn A K, Akinwande D, Zheng Y. Nano Lett., 2016, 16(1): 701.

[126]
Liu C X, Jiang D J, Zhu G Q, Li Z Z, Zhang X J, Tian P, Wang D, Wang E G, Ouyang H, Xiao M, Li Z. ACS Appl. Mater. Interfaces, 2022, 14(19): 22206.

[127]
Hendarto E, Gianchandani Y B. 2011 16th International Solid-State Sensors, Actuators and Microsystems Conference. June 5-9, 2011. Beijing, China. IEEE, 2011. 246.

[128]
Sun Y Y, Liu Y, Song B, Zhang H, Duan R M, Zhang D F, Dong B. Adv. Mater. Interfaces, 2019, 6(4): 1801965.

[129]
Song L, Cai J, Zhang S, Liu B, Zhao Y D, Chen W. Sensor Actuat. B-Chem., 2022, 358: 131523.

[130]
Lin X Y, Xu B R, Zhu H, Liu J R, Solovev A, Mei Y F. Research, 2020, 2020: 7659749.

[131]
Mo H Y, Yong Y M, Yu K, Chen W Q, Dai J L, Yang C. J. Comput. Phys., 2023, 481: 112037.

[132]
Zhang L D, Yuan Y H, Qiu X X, Zhang T, Chen Q, Huang X H. Langmuir, 2017, 33(44): 12609.

[133]
Zhang D N, Du X, Song X M, Wang H Z, Li X L, Jiang Y W, Wang M Y. SPE J., 2018, 23(3): 831.

[134]
Gallaire F, Meliga P, Laure P, Baroud C N. Phys. Fluids, 2014, 26(6): 062105.

[135]
Zhang L J, Zheng J, Wen B, Hu J. Sci. China Chem., 2024, 54(1): 85.

(张立娟, 郑晋, 文博, 胡钧. 中国科学: 化学, 2024, 54(1): 85.)

[136]
Jia F F, Sun K, Zhang P, Yin C C, Wang T Y. Phys. Rev. Fluids, 2020, 5(7): 073605.

Options
Outlines

/

〈 〉