

Theoretical Calculation and Computational Simulation on Electrolyte for Lithium Metal Battery
Received date: 2023-04-15
Revised date: 2023-08-23
Online published: 2023-09-10
Supported by
National Natural Science Foundation of China(52072105)
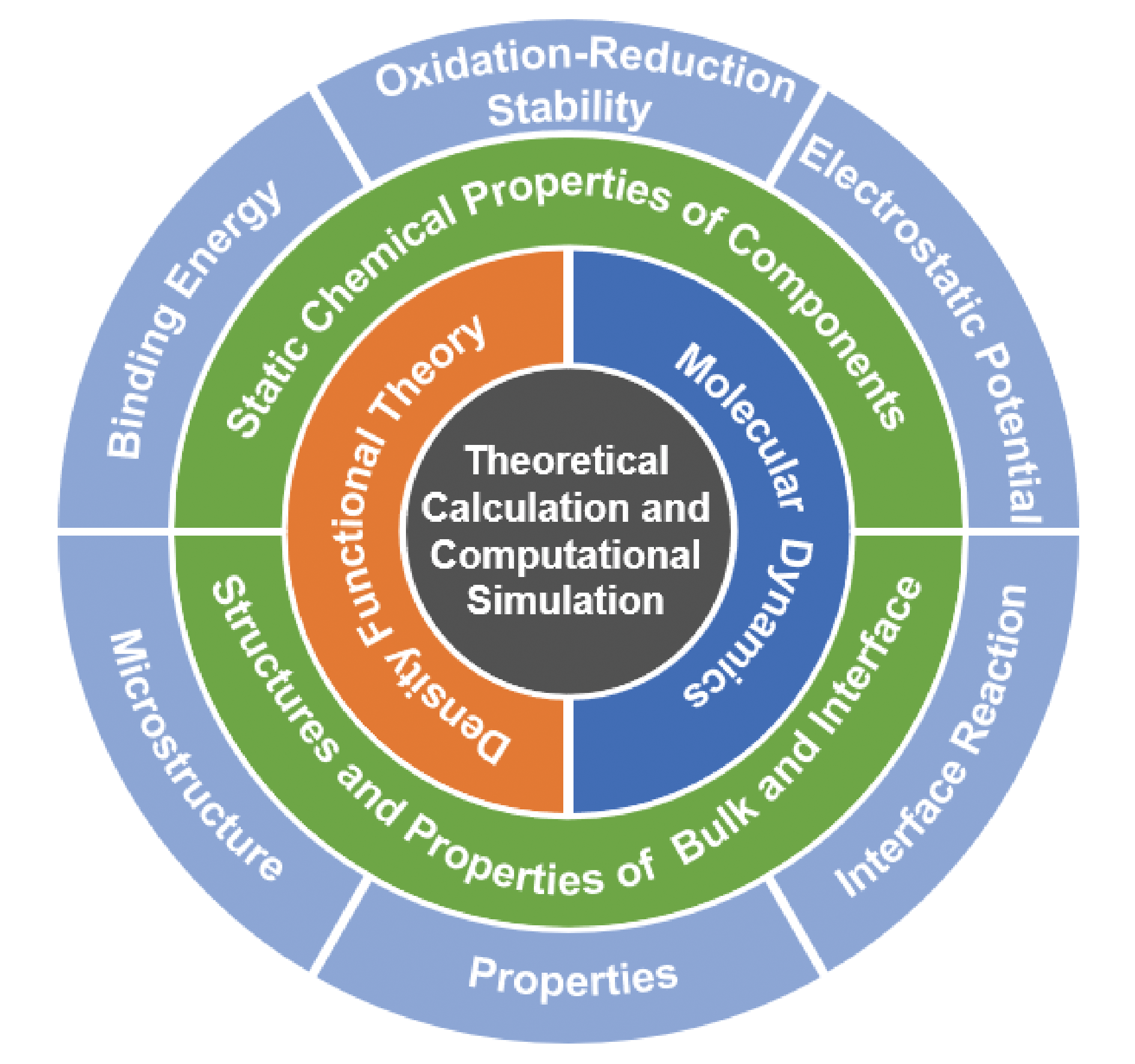
The regulation of electrolytes for the lithium-metal battery is of great significance in suppressing the growth of lithium dendrites. The traditional approaches mainly rely on empirical intuition and experimental trial and error, but less on computational simulation methods for high-throughput screen electrolyte formulations. Theoretical calculation and computational simulation can establish the relationship between the microscopic characteristics and macroscopic properties of electrolytes, guide electrolyte design, and predict electrolyte performance at the atomic scale, which play an indispensable role in the field of electrolyte research. This review aims to summarize the relevant progress of lithium-metal battery electrolytes in theoretical calculation and computational simulation. Firstly, the basic principles and calculating methods of quantum chemical calculation and molecular dynamics simulation for electrolyte research are introduced. Secondly, the application of the two simulation methods in the study involving the static chemical properties of electrolyte components, microstructure and properties of bulk electrolyte and electrode electrolyte interface are summarized, including binding energy in coordination complex, oxidation-reduction stability, electrostatic potential of electrolyte components, solvation structure, ionic conductivity, dielectric constant of bulk electrolyte, microstructure, properties and chemical reactions at the electrode electrolyte interface. Finally, the challenges and the way forward faced by theoretical calculation and computational simulation are discussed, providing new research ideas for the computational simulation of lithium-metal battery electrolytes.
1 Introduction
2 Methods of theoretical calculation
2.1 Calculation of quantum chemistry based on density functional theory theory
2.2 Molecular dynamics simulation
3 Static chemical properties of electrolyte components
3.1 Binding energy in coordination complex
3.2 Oxidation-reduction stability of electrolyte component
3.3 Electrostatic potential of electrolyte component
4 Microstructure and properties of bulk electrolyte and electrode electrolyte interface
4.1 Solvation structure of bulk electrolyte
4.2 Ionic conductivity of bulk electrolyte
4.3 Dielectric constant of bulk electrolyte
4.4 Microstructure and properties of electrode electrolyte interface
4.5 Reaction of anode electrolyte interface
5 Conclusion and outlook
Minghao Huang , Yueda Wang , Qian Hou , Hongfa Xiang . Theoretical Calculation and Computational Simulation on Electrolyte for Lithium Metal Battery[J]. Progress in Chemistry, 2023 , 35(12) : 1847 -1863 . DOI: 10.7536/PC230418
图1 (a) 室温(左)和低温(右)电解液中的基本相互作用及其结构-功能关系示意图[41];(b) 不同配位数下,DME和DMM与Li+的结合能[44];(c) 1 mol/L LiFSIDME电解液(左)和1 mol/L LiFSIDMM电解液(右)中Li金属表面Li+脱溶过程示意图[44]Fig. 1 (a) Schematic of fundamental interaction in room-temperature (left) and low-temperature (right) electrolytes, respectively, and related structure-function relationship[41]. Copyright 2023, John Wiley and Sons. (b) The plot of binding energies of Li+ solvated byDME andDMM as a function of coordination number[44]. (c) Schematic diagram of the Li+ desolvation process at Li metal surface in 1 mol/L LiFSIDME (left) and 1 mol/L LiFSIDMM (right) electrolyte[44]. Copyright 2022, John Wiley and Sons |
图2 在(a, b) 稀释和(c) 高浓度LiTFSA AN溶液上的量子力学DFT-MD模拟中,使用的模拟盒子和预测的态密度(PDOS)。所示结构是平衡轨迹的快照。对于稀溶液,考虑了LiTFSI盐的两种情况。PDOS剖面中的插图是传导带最低能级边缘的放大图[49]Fig. 2 Supercells used and projected density of states (PDOS) obtained in quantum mechanicalDFT-MD simulations on (a and b) dilute and (c) super-concentrated LiTFSA AN solutions. The illustrated structures are the snapshots in equilibrium trajectories. For a dilute solution, both situations of LiTFSI salt were considered. Insets in the PDOS profiles are magnified figures of the lowest energy-level edge of the conduction band[49]. Copyright 2014, American Chemical Society |
图4 (a)DME和DTDL的分子结构和静电势[60];(b) SCCE和CCE电解液中代表性溶剂化结构的静电势;(c) SCCE电解液中SEI形成示意图[61]Fig. 4 (a) Molecular structures and electrostatic potential ofDME andDTDL[60]. Copyright 2022, Springer Nature. (b) Electrostatic potential of representative solvation structures in SCCE and CCE electrolytes. (c) Schematic diagram of the formed SEI in SCCE electrolyte[61]. Copyright 2020, John Wiley and Sons |
图5 (a) Li+与不同阴离子中N原子之间的径向分布函数;(b~d) 35 m LiFSI、LiFTFSI、LiTFSI水系电解液代表性溶剂化结构的MD模拟快照[65]Fig. 5 (a) Radial distribution function between Li+ and N atom in different anion. (b~d) MD simulation snapshots of representative solvation structures in 35 m LiFSI, LiFTFSI, LiTFSI aqueous electrolytes[65]. Copyright 2020, American Chemical Society |
图7 (a) 离子电导率与盐浓度的关系[87];(b) 不同温度下(-15~60℃)电解液离子电导率的实验测试值和理论计算值[88]Fig. 7 (a) The relationship between ionic conductivity and salt concentration[87]. Copyright 2018, American Chemical Society. (b) Experimental and theoretical values of ionic conductivity of electrolyte at different temperatures (-15~60℃)[88]. Copyright 2022, Elsevier |
图8 (a) 温度对溶剂介电常数的影响;(b) 具有强分子间相互作用的混合溶剂的介电常数;(c) 具有弱分子间相互作用的混合溶剂的介电常数;(d) 浓度对电解液介电常数的影响[32]Fig. 8 (a) Effects of temperature on the dielectric constant of solvents;(b) dielectric constant of mixed solvents with strong intermolecular forces;(c) dielectric constant of mixed solvents with weak intermolecular forces;(d) effects of concentration on the dielectric constant of electrolytes[32]. Copyright 2021, John Wiley and Sons |
图9 (a) 1 mol/L LiFSIDME和(b) 1 mol/L LiFSI/LiNO3DME在0.5 V的正极表面内亥姆霍兹界面区局部结构[92],在213 K下,(c) 1 mol/L LiFSIDOL/DME和(d) 1 mol/L LiFSIDEE中Li+的去溶剂化过程示意图[93]Fig. 9 Local structure of inner-Helmholtz interfacial regions at cathode surface in (a) 1 mol/L LiFSIDME and (b) 1 mol/L LiFSI/LiNO3DME at 0.5 V[92]. Copyright 2022, Springer Nature. Visualized Li+ desolvation process at 213 K in (c) 1 mol/L LiFSIDOL/DME and (d) 1 mol/L LiFSIDEE[93]. Copyright 2022, American Chemical Society |
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|
| [33] |
|
| [34] |
|
| [35] |
|
| [36] |
|
| [37] |
|
| [38] |
|
| [39] |
|
| [40] |
|
| [41] |
|
| [42] |
|
| [43] |
|
| [44] |
|
| [45] |
|
| [46] |
WangD,
|
| [47] |
|
| [48] |
|
| [49] |
|
| [50] |
|
| [51] |
|
| [52] |
|
| [53] |
|
| [54] |
|
| [55] |
|
| [56] |
|
| [57] |
|
| [58] |
|
| [59] |
|
| [60] |
|
| [61] |
|
| [62] |
|
| [63] |
|
| [64] |
|
| [65] |
ReberD,
|
| [66] |
|
| [67] |
|
| [68] |
|
| [69] |
|
| [70] |
|
| [71] |
|
| [72] |
|
| [73] |
|
| [74] |
|
| [75] |
|
| [76] |
|
| [77] |
|
| [78] |
|
| [79] |
|
| [80] |
|
| [81] |
|
| [82] |
|
| [83] |
|
| [84] |
|
| [85] |
|
| [86] |
|
| [87] |
|
| [88] |
|
| [89] |
|
| [90] |
|
| [91] |
|
| [92] |
|
| [93] |
|
| [94] |
|
| [95] |
|
/
| 〈 |
|
〉 |